P3 - Álgebra Linear II – Questão 2
Considere o vetor e a reta passando pela origem cuja direção é dada pelo vetor . O vetor de mais próximo de possui norma igual a:
Passo 1
E aí, galerinha!
Como que foi essa P3 aí!?
O produtor tá aqui pra ajudar a responder todas as questões dessa prova!
Portanto, bora pra segunda questão!
Bora fazer um esboço do que tá acontecendo e o que é preciso para que um vetor esteja o mais próximo possível de :
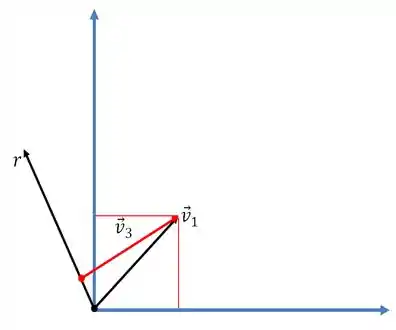
Passo 2
Bom! A gente tem que o vetor de mais próximo é dado por...
Pra que esse vetor esteja mais próximo possível de , é preciso que ele seja perpendicular a . Logo;
Essa reta, possui parametrização...
Pegando por exemplo um valor pequeno, , podemos calcular a norma desse vetor igual à...
E então, chegamos à nossa resposta, que é a alternativa (d). Poderiam ser as outras alternativas também, mas o que pede a questão é o menor valor!