Sejam os pontos e Pede-se:
- Mostrar que o triangulo é retângulo em
- Calcular a medida da projeção do cateto sobre a hipotenusa .
- Determinar o pé da altura do triangulo relativa ao vértice .
Passo 1
Temos que mostrar que o triângulo é retângulo em . Que pela figura a seguir, significa dizer que os vetores e formam entre si.
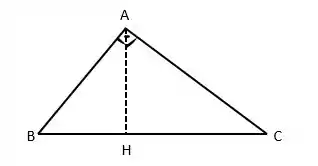
Se eles são ortogonais entre si, sabemos que . Assim, basta provar que o produto interno entre eles é ZERO.
Como nos foi dado os pontos e . Vamos achar os vetores e .
Então,
Portanto,
Passo 2
OMG!!! Projeção?? Nunca entendi essa parada!

Agora é a hora então!! Vamos passo a passo para você ficar fera em projeção ;).
Vimos na teoria, que projeção é a “sombra” que um vetor faz no outro. A figura a seguir ilustra melhor!
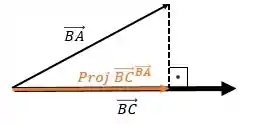
Então, o que o enunciado nos pede é o tamanho do vetor em laranja que o mesmo é a projeção do vetor sobre o vetor . Aqui vale enfatizar que o enunciado pediu o cateto , o cateto não indica um vetor e sim um lado, assim eu escolhi a direção do vetor . Como vimos na teoria, para achar o vetor projeção temos uma formulinha ;), que é:
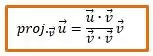
Para o nosso caso, essa fórmula fica da seguinte forma:
Vamos calcular os vetores que precisamos:
Então,
Achamos o vetor projeção, mas CUIDADO, não é isso que é nos pedido, ele pede a medida da projeção, ou seja, o tamanho. Assim, vamos calcular o módulo da projeção.
Passo 3
- Ufa!! Essa questão é longa hein!!!

Mais um pouquinho e já finalizamos haha
Agora, a questão nos pede para determinar o pé da altura relativa ao vértice . Mas, gente, quem é esse pé?

Hahahaha.... pé não é nesse sentido não heheh...na geometria, refere-se a “pé” ao ponto da extremidade oposta a referência. Por exemplo, nossa referência é o vértice , pois o enunciado pede em relação a ele. Então, o nosso pé na nossa figura é o ponto . Deu para sacar?
Bom, como vamos encontrar ? Bem, às vezes, ajuda pensar que uma questão com tantos itens um item tem a ver com o outro, principalmente em prova, em geral, o item depende do e assim por diante (CUIDADO: não tome como regra, mas sempre vale prestar atenção que pode poupar tempo se isso for verdade).
Se olharmos para a figura, vamos perceber que a projeção que calculamos no item nada mais é que o vetor . Opaaaa, apareceu o !!!
Então, pelo item temos que:
Temos o ponto , que nos foi dado, certo?? Então,
Vamos supor que nosso é
Igualando os lados, temos:
Finalmente,
Nossa, essa foi pesada hein, mas conseguimos!!!!

Resposta
b)
c)