Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada – Casos Clássicos

Ver Teoria
Exercício 41235678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758

Enunciado

Um balão eleva-se verticalmente do solo à razão de 3   m/s . Quando o balão está a 48   m do solo, passa exatamente sob ele um automóvel viajando à velocidade de 20   m/s . Com que velocidade varia, 4 segundos após, a distância entre eles?

Passo 1

Vamos desenhar o problema:

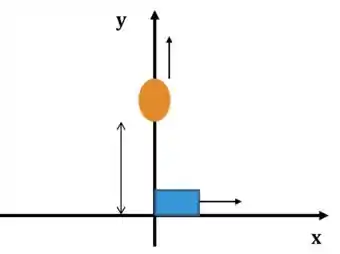
Agora a gente precisa determinar o que a gente tem que achar aí. O problema quer saber a variação da distância entre eles. Se a distância é s então queremos saber:

d s d t = ? ?

Passo 2

Agora precisamos ver o que a gente tem. O balão se eleva verticalmente à razão de 3   m/s . Isso é a velocidade vertical. Se a posição é y então:

d y d t = 3 m / s

Não se engane com relação a y . O valor inicial de y é 48 m . Para instantes seguintes teremos que:

y t = y 0 + v t ⟹ y t = 48 + 3 t

No instante 4 :

y 4 = 48 + 3 ⋅ 4 = 48 + 12 = 60 m

Temos também a velocidade do carro, que está andando horizontalmente. Sendo x a posição horizontal:

d x d t = 20 m / s

O que vai relacionar isso tudo? Pitágoras!

s ² = x 2 + y 2 ⟹ 2 s ⋅ d s d t = 2 x ⋅ d x d t + 2 y ⋅ d y d t ⟹ s ⋅ d s d t = x ⋅ d x d t + y ⋅ d y d t

Substituindo tudo que a gente sabe:

s ⋅ d s d t = x ⋅ 20 + 60 ⋅ 3 ⟹ s ⋅ d s d t = 20 x + 180

Passo 3

E agora? Se o carro estava andando a 20   m/s então sua posição será:

x t = 20 t

No ponto que a gente quer: x 4 = 20 ⋅ 4 = 80 m

E s ? Quando x = 80 m :

s ² = x 2 + y 2 ⟹ s 2 = 80 2 + 60 2 ⟹ s = 100

Agora é só felicidade. Vamos substituir tudo:

s ⋅ d s d t = 20 x + 180 ⟹ 100 ⋅ d s d t = 20 ⋅ 80 + 180 ⟹ 100 ⋅ d s d t = 1780

d s d t = 1780 100 ⟹ d s d t = 17.8   m / s

Resposta

d s d t = 17,80   m/s

Exercícios de Livros Relacionados

Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand
30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca