UFRJ – Cálculo 1 – Lista 8 – Questão 6
O raio de luz de um farol, que está situado a 3 km de uma praia reta, faz 8 rpm (rotações por minuto). Considere a altura do farol desprezível em relação a sua distância até a praia. Determine a velocidade da extremidade do raio de luz, ao longo da praia, quando ele faz um ângulo de 45° com a linha da praia.
Passo 1
A primeira coisa é fazer um desenho da situação pra entender o problema.
Vamos chamar de D o comprimento do raio de luz, e de a distância ao longo da praia que ele percorreu em relação àquela linha tracejada. Vai ficar assim:
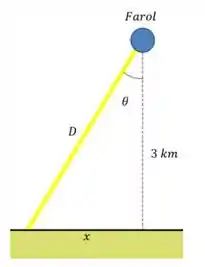
Aquele é o ângulo entre o raio de luz e a linha tracejada, não é o ângulo com a praia, eu fiz isso porque a conta fica mais simples assim a velocidade que ele dá é desse ângulo e não do da praia, só lembrar que:
Isso nos dá duas relações:
Passo 2
Tendo essas relações vamos derivar isso tudo em relação ao tempo:
Temos as duas relações mas quais dessas taxas de variação nós queremos? Lembra que ele quer a velocidade do raio de luz ao longo da praia? Então ele quer
Precisamos ver agora se temos todos os valores pra substituir ali. Primeiro ele deu a velocidade angular:
Ele também deu o ângulo:
Como ele quer vamos isolar na primeira equação, porque na primeira? A segunda tem a relação com e
Falta acharmos D e x e aí ser feliz 😊
Passo 3
Como o ângulo é 45° esse triangulo é isóscele, dessa forma:
E podemos fazer
Passo 4
Vamos substituir todos os valores