Um velocista corre em uma pista circular de raio . Seu amigo está parado a uma distância de do centro da pista. Em um certo instante, quando a distância entre eles é de , o velocista está se afastando do amigo a uma velocidades de de volta por minuto. Quão rápido a distância entre os amigos está variando nesse momento?
Passo 1
Vamos pensar em como organizar o problema, em primeiro lugar. Nota que a velocidade que ele nos dá é em voltas por minuto, ou seja, uma velocidade angular. Daí a gente tira a informação de que o ângulo é um parâmetro importante a ser analisado. Agora vamos desenhar as distâncias do problema, lembrando que o que buscamos é, em suma, a distância entre o velocista e o amigo:
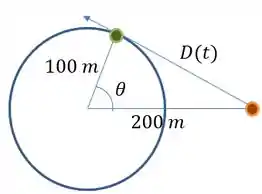
Essa seria a organização do que se passa, onde é a distância entre as pessoas e o ângulo entre as retas que ligam o velocista e o amigo ao centro. Nosso objetivo é achar a variação da distância entre os caras, ou seja, .
Passo 2
Nós temos que num dado instante a distância vale e vale . Vamos primeiro achar um jeito de equacionar a relação entre as duas grandezas. O melhor jeito me parece ser usando a Lei dos Cossenos:
Onde, se derivarmos, acharíamos o seguinte:
Nossas equações serão, portanto:
Passo 3
Se em temos e , vamos substituir no sistema e achar o :
Se temos , sabemos que . Logo,
Logo,