UFMG – Cálculo I – P2 – 2021.1
Um holofote sobre o chão ilumina uma parede de m distante dele. Se um homem de m de altura anda do holofote em direção à parede a uma velocidade de m/s, quão rápido descreve o comprimento de sua sombra sobre a parede quando ele está a m dela?
Passo 1
E aí, gente!! Beleza? Nessas questões é sempre bom a gente primeiro tentar desenhar e escrever as funções que descrevem esse problema físico. Então sempre façam isso antes de sair resolvendo o problema.
Vamos chamar a distância do homem ao holofote de e a distância do homem a parede de .
É importante lembrar que se a distância do holofote à parede é de m, então
Passo 2
A sombra do homem é projetada sobre a parede, descrevendo uma situação de semelhança de triângulos. Se chamarmos de , a altura da sombra, temos a seguinte situação:
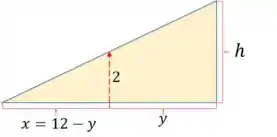
Logo, por semelhança de triângulos:
Passo 3
Logo, para achar a taxa com que varia, é só encontrar a sua derivada em função do tempo:
Quando e , e o homem caminha no sentido de crescimento de a uma taxa de m/s, então:
Logo, o comprimento da sombra decresce (por conta do sinal negativo) a uma razão de m/s.
Resposta
O comprimento da sombra decresce a uma razão de m/s.