Taxas Relacionadas
Dois lados de um triângulo têm comprimentos fixos, e , respectivamente. O ângulo entre estes lados está crescendo à taxa de . Encontre a taxa segundo à qual a área do triângulo está crescendo quando o ângulo entre os lado de comprimento fixo é .
Passo 1
Vamos lá, esboçando agora a situação:
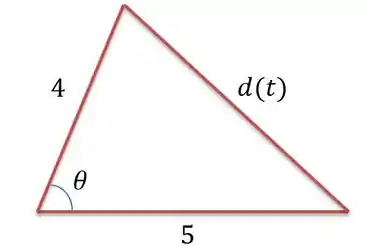
Agora, independente desse lado , que varia com o tempo, temos por definição que a área do triângulo, que varia com o tempo, é dada por:
Onde é o ângulo entre os lados e e também varia com o tempo. Assim, a relação fica:
Assim, derivamos ambos os lados em relação ao tempo:
Se cresce a uma taxa constante de , quando nós temos a seguinte :
Resposta
Exercícios de Livros Relacionados
Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand
30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca