Uma roda gigante tem de raio e seu centro está a do solo. Ela gira no sentido anti-horário. Seja um ponto fixado nessa roda. No instante em que está a do solo, a distância de ao solo varia a uma taxa de .
A que taxa a roda está girando no instante ? (Ou seja, qual é a taxa de variação de em relação ao tempo no instante ?)
Do ponto parte um raio de luz que tangencia a circunferência e ilumina um ponto no solo. Qual é a taxa de variação da distância do ponto ao ponto que ele ilumina no solo no instante ?
Passo 1
Dei uma esquematizada na situação, adicionando ao desenho uma grade de eixos :
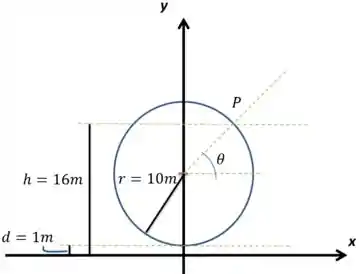
Olha comigo, botei passando pelo eixo do círculo, que está a e tem . Bom, pela situação, o que é a minha altura em função do tempo? A distância de até o eixo (o chão), ou seja, minha altura é ! A partir disso temos que descobrir relação entre e para então descobrir a taxa de giro, o . Olha, está sempre a de , já que o centro do círculo está elevado dessa mesma distância. Em relação ao eixo, o varia como se fosse um círculo trigonométrico, ou seja, , onde já temos o raio. No fim das contas a equação de em relação a é essa:
Deriva dos dois lados para relacionar uma taxa com a outra:
Sabemos ainda que nesse momento temos :
Voltando para a outra equação, podemos apenas jogar isso e e terminamos:
Passo 2
Agora a parada é outra, acompanha no desenho:
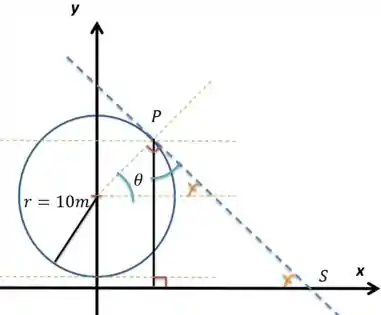
Repara que se eu traçar essa reta tangente, posso jogar a altura do ponto ali e formar um ângulo reto com o eixo . Nessa situação, observando a horizontal aonde eu começo o ângulo e a reta tangente ao círculo, percebo que os dois ângulos laranjas são iguais, já que a reta de é paralela ao eixo . Sendo assim, comparando os dois triângulos com ângulos retos e laranjas, descubro aquele ângulo azul claro que terá o mesmo valor e variação de .
No triângula maior, posso chamar a distância de ao ponto iluminado de . Sendo a altura igual a e o ângulo entre e valendo , descubro essa relação:
Deriva para comparar as taxas:
Se em temos , , , , , logo: