UFABC – Cálculo 1 – Lista 3 – 4
Uma esteira transportadora está descarregando cascalho de , constituindo uma pilha na forma de cone com o diâmetro da base e altura sempre igual. Quão rápido cresce a altura da pilha quando está a de altura?
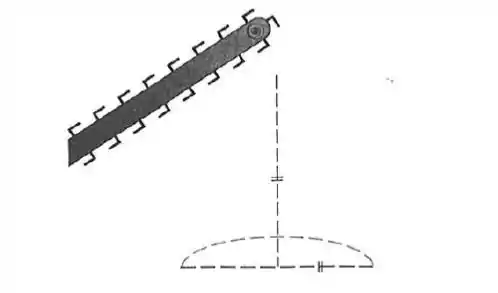
Passo 1
O volume da pilha de cascalho de altura e raio é dada por:
Como o diâmetro da base que é o dobro do raio é sempre igual à altura, então:
Então, o volume é dado por:
Passo 2
Derivando em função do tempo em minutos, temos:
Então, quando metros e .
Logo, a altura varia a uma razão de metros por minuto.
Resposta
A altura varia a uma razão de metros por minuto.
Exercícios de Livros Relacionados
Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand
30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca