Taxas Relacionadas
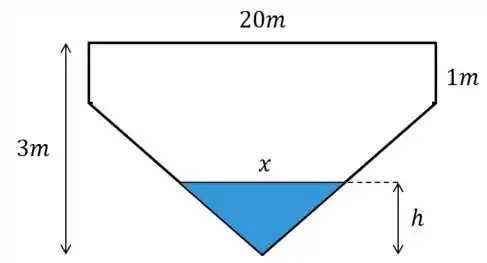
Uma cisterna de de largura, de comprimento, de profundidade nas extremidades e no meio, de modo que o fundo seja formado por dois planos inclinados (veja a figura). Despeja-se água na cisterna a uma taxa de . Seja a altura do nível da água em relação à parte mais profunda. Com que velocidade (em metros por minuto) estará subindo no instante em que ?
Passo 1
Comecemos a análise por uma variável cuja variação nós temos, o volume:
Para isso, precisamos da fórmula do volume, que é:
A área da base, por ser um triângulo, é calculada da forma abaixo:
Passo 2
Dessa forma, a derivada que nós queremos é dada pela regra do produto:
E desejamos isto num instante :
Podemos relacionar as nossas variáveis por uma semelhança de triângulos:
De forma que:
Então, substituindo:
Passo 3
Substituindo os dados: