Considere a parábola .
I – Encontre a equação da reta tangente à parábola no ponto
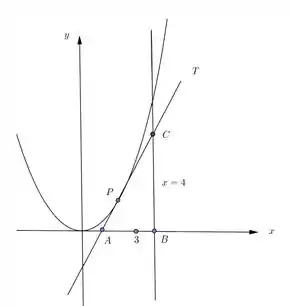
II – Expresse a área do triangulo ABC em função de (ver figura).
III – Sabendo que o ponto parte da origem e que a taxa de variação da abscissa é , determine a taxa de variação da área do triângulo ABC, quando o ponto de tangência é .
Passo 1
Show. Vamos fazer uma parte de cada vez. Primeiramente, a questão quer a reta tangente num ponto geral . E equação da reta então será:
Vamos calcular para substituir ali em cima. Para tal, derivamos e substituímos o ponto:
Legal, então vai ficar:
Isolando :
Passo 2
Agora precisamos expressão a área do triângulo formado pela reta tangente, a reta e ou eixo , como mostra a figura. A área de um triângulo é:
Ou seja, base vezes altura divido por . Precisamos então da base e da altura.
Vamos tentar achar a base. Olhe lá e veja que o ponto é justamente onde a reta cruza o eixo , ou seja, quando . Assim:
Dessa maneira, como aparece na reta , a distância é a nossa base:
Temos a base, agora precisamos saber qual é a altura. Veja que acontece justamente quando a reta corta a outra reta , ou seja, em:
Assim, a distância será a nossa altura:
Já temos a base e altura, então chegamos na área:
Passo 3
A questão tenta confundir aqui, muita gente não lembra que a abcissa é justamente o eixo fique atento. O problema pede a taxa de variação dá área, então vamos voltar a expressão:
Derivando no tempo já achamos a fórmula dessa variação. Pela regra do produto:
A taxa de variação de é , mas temos o ponto dado . Ou seja, , e, portanto: . Além disso, para , temos . Substituindo isso tudo:
No gabarito oficial, a resposta está em , mas como o enunciado tá , então essa é a unidade correta, não esqueça de colocá-la no final!