Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada – Casos Clássicos

Ver Teoria
Exercício 56123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555758

Enunciado

Taxas Relacionadas

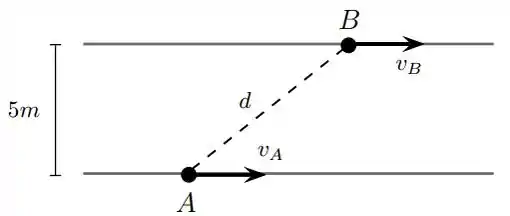
Dois caminhos retilíneos paralelos distam de 5 metros . Os objetos A e B deslocam-se sobre os caminhos com velocidades v A t e v B t , respectivamente. Em um certo instante t 0 , a distancia d entre eles é de 13   m , A tem velocidade v A t 0 = 5   m / s e B tem velocidade v B t 0 = 2   m / s , conforme a figura. Determine d ' t 0 , a velocidade com que eles estão se aproximando.

Passo 1

Em um problema de taxas relacionadas, devemos primeiro fazer um desenho para nos ajudar a descobrir as relações matemáticas que podemos tirar do problema.

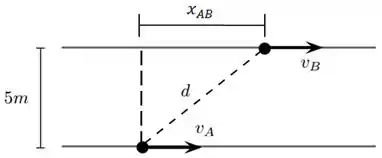
Chamei de x A B a distância horizontal entre as partículas.

Passo 2

Usando o teorema de Pitágoras

d 2 = x A B 2 + 5 2

Onde x A B = x B - x A

Derivando essa equação em relação ao tempo teremos

2 d d ' = 2 x A B x A B '

Onde x A B ' é

x A B ' = x B ' - x A ' = v B - v A

Lembre que

d ' = d d t d

x A B ' = d d t x A B

Passo 3

No momento que ele pediu temos os seguintes dados

d = 13   m x A B ' = 2 - 5 = - 3   m / s

Falta encontrarmos x A B , pela equação dele com d

13 2 = x A B 2 + 5 2

x A B 2 = 169 - 25 = 144

x A B = 12   m

Passo 4

Substituindo tudo teremos

2 d d ' = 2 x A B x A B '

2 ⋅ 13 ⋅ d ' = 2 ⋅ 12 ⋅ - 3

d ' = - 36 13   m / s

Essa resposta deu negativa porque a distância está diminuindo, não se assuste com esse sinal isso só quer dizer que eles estão se aproximando. Como ele quer saber a velocidade que eles estão se aproximando ele quer o módulo, assim eles se aproximam com velocidade 36 / 13

Resposta

Eles se aproximam com velocidade 36 13   m / s

Exercícios de Livros Relacionados

Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand
30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca