Taxas Relacionadas
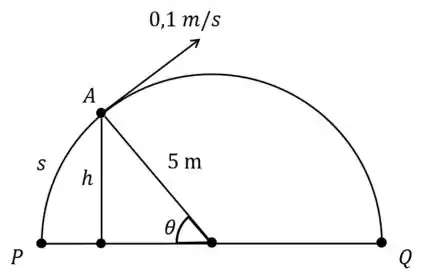
No desenho, o ponto representa um objeto que se desloca sobre uma semicircunferência de raio , com velocidade constante . Em cada instante, é a distância de até o diâmetro .
Durante o movimento de subida, qual será a taxa de variação da distância no momento em que ela medir ?
Passo 1
O que a questão pede é a grandeza:
No instante em que . O dado que nós temos é referente à velocidade.
Como a velocidade é a taxa de variação da posição com relação ao tempo, e o espaço transladado pela partícula em é o arco , então é seguro dizer que a velocidade é:
Passo 2
A grandeza que vai conectar os nossos e vai ser o ângulo que é comum à geometria dessas duas grandezas. Pelas equações da geometria:
Temos também que o raio é:
Passo 3
Derivando em relação ao tempo:
A grandeza comum a ambas as equações nós evidenciamos em vermelho acima e podemos substituir. Na primeira equação, temos:
Substituindo na segunda:
Passo 4
Agora basta achar quanto é o quando :
Da figura, temos, quando
Calculando:
Portanto, substituímos: