Uma barra, representada na figura pelo segmento , tem a extremidade apoiada em uma plano inclinado e a extremidade no chão conforme a figura. No instante a barra desliza de modo que o segmento mede e diminui a uma taxa de variação de s. Sabendo que o segmento mede no instante , determine a taxa de variação de neste instante.
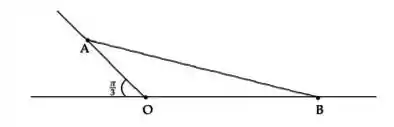
Passo 1
A equação que melhor relaciona os lados e um ângulo conhecido pela figura é a Lei dos Cossenos:
Onde temos que o ângulo , onde . Vamos chamar , e , para simplificar na hora de escrever. Desejamos saber a taxa de variação de em função da taxa de . Sabemos que, no instante , temos:
Como a barra não pode mudar de configuração, sabemos que é constante, ou seja, em qualquer instante. Assim, podemos derivar a Lei dos Cossenos e substituir os valores em para descobrir o valor de nesse mesmo instante:
Assim, a taxa de variação do lado , o lado , é .