UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 4.4a
Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a
escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela
escorrega a uma taxa de 5 pés/s.
(a) A que taxa o topo da escada escorrega para baixo nesse momento?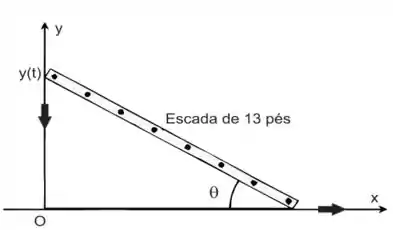
Passo 1
Eaew, belezinha?
A questão nos pede para calcular a taxa que o topo de uma escada de 13 pés escorrega pela parede. Como a escada possui um tamanho fixo, há um vínculo entre a medida da distância do topo da escada ao chão e a distância horizontal da base da escada. Da figura, é simples perceber que esse vínculo pode ser escrito através do teorema de Pitágoras se notarmos que a escada, a distância vertical e a distância horizontal constituem, respectivamente, a hipotenusa e os catetos. Assim, podemos escrever a restrição das medidas na seguinte forma:
Sabendo que as distâncias x(t) e y(t) variam no tempo, mas o comprimento da escada não varia e, sabendo também que, a cada instante de tempo as distâncias formarão um novo triângulo retângulo, podemos calcular suas taxas de variações derivando a expressão. Então, vamos lá!
Passo 2
Escrevendo a componente y(t) em função da componente x(t), obtemos:
Para descobrir como a altura do topo varia com o tempo, derivamos a expressão acima em relação ao tempo, utilizando a regra da cadeia. Definindo as funções e podemos escrever a função y(t) como . Assim, temos que a derivada da altura em relação ao tempo é:
Como a questão quer saber qual a taxa o topo escorrega quando a base da escada está a uma distância de x(t) = 12 pés e, como nesse momento, a taxa de variação da base é de 5 pés/s, só precisamos substituir esses valores na expressão acima para determinar y’(t). Logo, temos
Como esperado, a taxa de variação do topo é negativa, já que a escada está escorregando pela parede e com isso, a medida y(t) diminui com o tempo.