Selecionado da Lista de Derivadas da Professora Renata - Cálculo 1 - UERJ
Um homem com de altura caminha em direção a um edifício, com uma velocidade de . Se existe um ponto de luz no chão a do edifício, com que velocidade a sombra do homem estará diminuindo, quando ele estiver a do edifício?
Passo 1
Vamos desenhando:
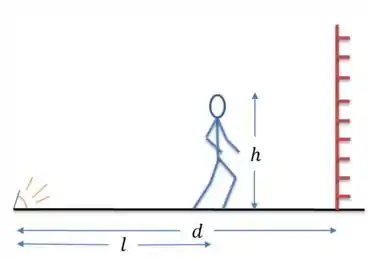
Bom, chamando a altura do cara de , a distância do ponto até a parede de e do ponto até o homem de . Repare, quando falamos na velocidade do cara, estamos, basicamente, falando da velocidade com que aumenta. Colocando, então tudo o que o cara me passou como dados, fica assim:
E ele quer saber, quando como varia a altura da sombra do maluco aí. Que é basicamente:
Passo 2
Vamos “matematicar” esse desenho:
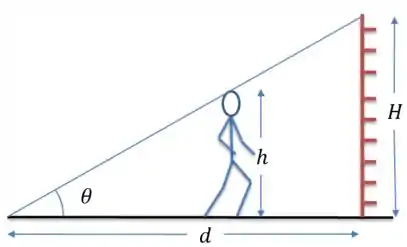
Onde a sombra tem altura . Repara que a inclinação que marcamos ali varia, é maior quando ele está mais perto do ponto e menor quando ele se afasta. O que não muda é essa relação entre as alturas e as distâncias que, por Semelhança de Triângulos, fica desse jeito:
Bom, pegando aquilo que já conhecemos, podemos deixar o em função do :
Passo 3
Repara no seguinte, tanto a altura quando a distância variam com o tempo. Se derivarmos em relação ao tempo ambas grandezas, podemos construir uma relação entre as taxas:
Queremos essa taxa quando ele estiver a da parede vamos ter:
Assim
Sabendo ainda que a taxa de variação vale, em qualquer momento, a mesma coisa:
Substituindo, portanto:
E é isso!