Um cilindro circular reto está inscrito em uma esfera. Se o raio da esfera cresce a uma taxa de e o raio da base do cilindro cresce a uma taxa de , com que razão está variando a área lateral do cilindro no momento em que o raio da esfera é e o raio da base do cilindro é de ?
Passo 1
O que a gente quer achar? Queremos calcular a variação da área lateral do cilindro:
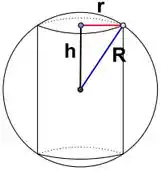
Chamando, como na figura, de o raio da esfera, o do cilindro e a metade da altura, vamos reunir aqui os dados num instante dado que eu vou chamar de :
Passo 2
E ele quer saber, com isso, como varia a área lateral do cilindro. Bom, podemos calcular essa área pela definição geométrica dela, que é a seguinte:
Porém, é uma variável da qual não conhecemos a taxa de variação e o valor em , o que complica para trabalhar. Por outro lado, dá para ver pela própria figura que e formam um triângulo retângulo, então poderemos escrever em função de e :
Substituindo:
Passo 3
Vamos derivar os dois lados em função do tempo e ver como ficamos (não se esqueça da regra do produto, heim):
Derivando a raiz e aplicando a regra da cadeia...
Bom, em a gente sabe quais serão os valores de , , e .
Agora é só substituir tudo o que temos mesmo...