Uma câmara de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação , sendo a altura e o tempo. A câmara está a do local de lançamento. Encontre a taxa de variação da distância entre a câmara e a base do ônibus espacial, 10 segundos após o lançamento (suponha que a câmara e a base do ônibus estão no mesmo nível no tempo ).
Passo 1
O esquema abaixo representa a situação descrita no enunciado 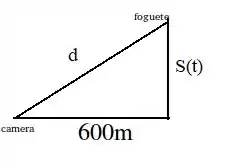
Queremos a taxa de variação da distância quando . Para isso, precisamos de uma relação entre e . Essa relação pode ser tirada da figura acima, que representa um triangulo retângulo.
Passo 2
Derivando implicitamente a equação acima temos:
Passo 3
Agora só precisamos substituir e . Vamos começar por e . Quando temos que
E
Por fim, vamos achar derivando a expressão de .
Como ,
Finalmente: