Da janela de um prédio, a metros do solo, um menino brinca com uma ponteira laser, movendo-a verticalmente e iluminando a parede do prédio vizinho, situado a uma distância de metros. Num determinado instante, o ponto de luz está a uma altura de metros e a velocidade com que ele sobe é de metros por segundo. Determine a taxa de variação do ângulo formado entre a horizontal e o feixe de luz nesse instante.

Dei uma esboçada no que está acontecendo aí nessa situação:

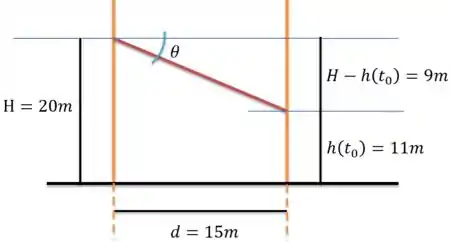
O quele pede é a taxa de variação do ângulo entre horizontal e o raio de luz, o do desenho. A gente pode concordar que, independente de e da altura , a razão entre e valerá sempre , pelo que o desenho nos mostra:

Bom, e . Aliás, essa velocidade com que o raio sobe que ele disse é a variação da altura em relação ao solo. No instante dado , temos que . Reunindo isso tudo eu posso usar na minha equação e já derivá-la para relacionar variação de com :

Agora, para determinar a derivada de no instante dado eu preciso da secante nesse instante. Vamos voltar ao desenho, será dado por dividido pela hipotenusa que é dada pelo seguinte, segundo o Teorema de Pitágoras:

Certo, tendo isso podemos pensar no cosseno, lembrando ainda que secante é o inverso do cosseno:

Vamos voltar para a equação substituindo tudo que já sabemos: