Unb - Cálculo 1 - Listas - Lista 8 - Exercício 6
Uma escada de está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Passo 1
Olá pessoal, como vai a vida? Espero que esteja bem! Vamos pra mais uma questão??
Essa é bem clássica hein, bom temos uma escada de . Essa escada está encostada em uma parede, em seguida essa escada é afastada em sua extremidade inferior a uma velocidade de , então deseja-se saber qual é a velocidade na extremidade superior quando essa escada distar da parede. Belezura, então a nossa situação é a da imagem seguinte:
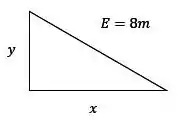
Onde representa o tamanho da escada, representa a altura da extremidade superior em relação ao pé da parede e por fim, que representa a distância da extremidade inferior da escada ao pé da parede. E aí? O que podemos fazer agora?
Passo 2
Bom, pela imagem do passo anterior vemos que é possível relacionar as distâncias aplicando o teorema de Pitágoras. Assim,
Sendo que
Passo 3
Como desejamos saber a velocidade da ponta superior da escada quando , e é importante lembrar que a velocidade é a derivada da posição em relação ao tempo. Nesse caso deveremos aplicar a derivação implícita na equação anterior para que possamos encontrar o desejado. Sendo assim,
Já sabemos o valor de , o enunciado nos forneceu também quanto varia o em relação ao tempo (. Logo basta encontrarmos o valor de para aplicarmos na expressão encontrada. Se e então será:
Passo 4
Agora já temos tudo para aplicar na nossa receitinha de bolo, bora lá!
Queremos encontrar o valor de uma vez que a velocidade da escada na extremidade superior é a taxa de variação da distância em um dado tempo.
E aí? Consegui te ajudar? Beleza!
Bora continuar treinando! :)