Um retângulo possui lados que variam com o tempo e está inscrito numa região triangular conforme a figura abaixo. Determine com que taxa a área do retângulo está variando no instante em que sua altura mede e está aumentando à taxa de . Neste instante a área está aumentando ou diminuindo?
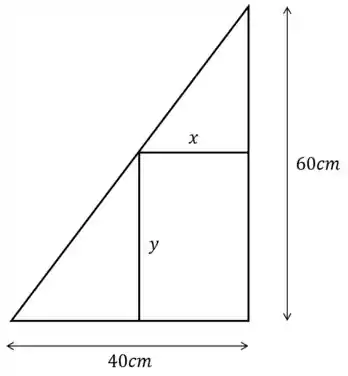
Passo 1
O problema quer saber a taxa com que a área do retângulo varia. Então ele quer:
Ele também nos disse que para o instante tratado, e
Passo 2
Podemos usar a expressão da área do retângulo para relacionar as variáveis do problema:
A expressão da área é:
Precisamos então derivar:
Substituindo o que a gente já sabe:
Passo 3
Precisamos de sua derivada. Mas temos que, por semelhança de triângulos:
Derivando ambos os lados:
Substituindo:
No momento em que a altura vale , temos:
Portanto, substituindo de volta na fórmula de :
Resposta
A taxa de variação da área é negativa e, portanto, a área do retângulo está diminuindo.