Taxas Relacionadas
O sol está se pondo com ângulo de elevação (ângulo entre os raios e uma reta horizontal) que diminui a uma taxa de radianos/hora. Com que velocidade estará crescendo a sombra de um prédio de metros de altura quando o ângulo de elevação do sol for ?
Passo 1
Em um problema de taxas relacionadas, devemos primeiro fazer um desenho para nos ajudar a descobrir as relações matemáticas que podemos tirar do problema.
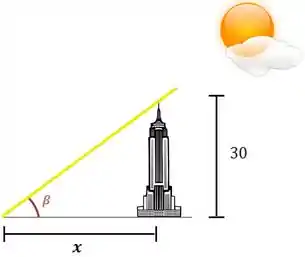
Passo 2
Usando trigonometria
Derivando vamos ter
Passo 3
Para resolvermos essa equação devemos ter todos os dados menos . Do enunciado
Precisamos achar
Passo 4
Substituindo os valores na equação das variações
Resposta
Exercícios de Livros Relacionados
Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand
30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca