(Enunciado adaptado em relação à prova original)
Considerando todos os trapézios regulares de área e tendo os seus menores ângulos internos valendo , calcule o menor valor possível de perímetro, nessas condições.
Passo 1
Vou começar esboçando a situação:
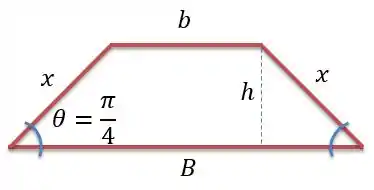
Esse seria um triângulo qualquer de acordo com as especificações da questão. A gente sabe que as suas área e perímetro, chamando as bases de (maior) e (menor), a altura de e os lados inclinados de , seriam dadas por:
Agora, na função que queremos otimizar, o perímetro, nós temos variáveis. Precisamos através de relações entre as variáveis chegar a uma fórmula de uma só variável.
Passo 2
Em primeiro lugar, vamos eliminar a altura da fórmula da área:
Temos uma relação nesse trapézio entre os lados seguindo que a base menor somada às projeções horizontais dos lados inclinados tem que ser iguais a base maior, se o trapézio for regular. Como a questão já disse que ele é realmente regular:
Agora, na própria fórmula da área temos uma outra igualdade entre as variáveis, já que a área sempre valerá :
Podemos substituir a altura e a base em função de e , como já achamos:
Então vamos voltar ao termo do perímetro e tentar colocar tudo em função de :
Achamos, finalmente, a nossa fórmula para o perímetro!
Passo 3
Agora a gente deriva e iguala a para ver qual é o que otimiza isso tudo:
Ao substituir valores menores que para , vemos que o sinal de é negativo, bem como para valores maiores que o o termo da derivada é positivo. Isso faz com que o ponto seja de mínimo local na função .
Esse é o que gera perímetro mínimo. Assim, o perímetro mínimo será: