Exercícios Resolvidos de Taxa Relacionada – Casos Clássicos

Ver Teoria

Exercício 29 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

Enunciado

UFABC – Cálculo 1 – Lista 3 – 2

Dois carros iniciam o movimento de um mesmo ponto. Um viaja para o sul a 60 mi/h, e o outro para o oeste a 25 mi/h. A que taxa está crescendo a distância entre os carros duas horas depois?

Passo 1

E aí, galera!!!! Tudo bem com vocês? Vamos analisar o que nosso probleminha está falando. Bom, ele nos diz que tem dois carrinhos que saem no mesmo momento e de um mesmo ponto, mas um segue pro sul e o outro pro oeste, cada um com a sua velocidade. Depois de nos falar isso, ele nos pede a variação da distância entre eles depois de duas horas da partida. Viu, nem é tão difícil assim. Eaii, partiu??

Passo 2

Nosso primeiro passo vai ser definir as nossas variáveis do problema.

Temos a velocidade do carrinho que vai pra oeste

E a velocidade do carrinho que vai pro sul

Bom, nós queremos saber como varia a distância entre os carrinhos. Podemos dizer que é a variação da nossa hipotenusa, uma vez que teremos os catetos equivalendo aos deslocamentos de cada um dos carrinhos.

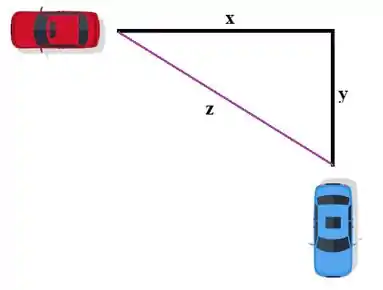
Se a distância entre os carrinhos é , então temos a seguinte variação para achar:

Passo 3

Já vimos que é um triângulo retângulo, então nos resta aplicar Pitágoras e a derivada direta.

Derivando implicitamente com relação a

Agora é só substituir os valores pra gente encontrar

Para 2 horas, temos:

Logo:

Resposta

Exercícios de Livros Relacionados

Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma

37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?

39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.

Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand

30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca