UFRJ – Cálculo 1 – Lista 8 – Questão 4
Uma escada de 8m está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de 2 m/s, com que velocidade a extremidade superior estará descendo no instante em que a extremidade inferior estiver a 3m da parede?
Passo 1
O primeiro passo é a gente desenhar o problema.
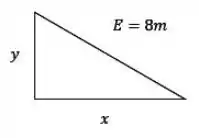
Chamamos o comprimento da escada de E, a distância da ponta inferior da escada à parede de x e a altura de y. Podemos relacionar essas duas grandezas usando Pitágoras, certo?
Passo 2
Já que queremos a velocidade com que a ponta superior da escada desce no momento em que precisamos derivar implicitamente a relação encontrada, visto que a velocidade é uma taxa, ou seja, uma derivada, da distância em relação ao tempo. Portanto, o que queremos encontrar é quando e
Aqui temos um pequeno problema. Para encontrar precisamos do valor de , mas isso pode ser facilmente obtido se substituirmos o valor de na equação .
E voltando para encontrar teremos:
O sinal de negativo na velocidade indica que a escada está descendo.