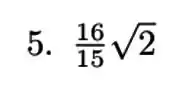
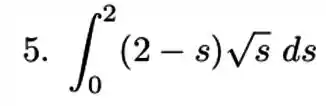
Passo 1
Vamos trabalhar um pouco nessa integral pra facilitar nossa vida. A forma mais simples é separar essa expressão em duas integrais.
Tirando as constantes e lembrando que , então nossas integrais vão ser
Passo 2
Agora podemos resolver as integrais separadamente
Aplicando os limites
Na segunda integral
Passo 3
Resolvidas as integrais, vamos aplicar os resultados na expressão que encontramos lá no primeiro passo.
Resposta
Exercícios de Livros Relacionados
Ache a integral indefinida geral. ∫ v v 2 + 2 2 d x
Ache a integral indefinida geral.12 . int (x^2 + 1 + (1)/(x^2 + 1)) d x
Ache a integral indefinida geral ∫ c o s s e c 2 t - 2 e t . d t
Ache a integral indefinida geral.15 . int (theta - csc theta cot theta) d theta
Calcule os momentos M x e M y e o centro de massa de uma lâmina com a densidade e o formato dados