Calcule a integral de linha escalar
Onde é a parte da curva entre os pontos e .
Passo 1
A gente já sabe que para resolver uma integral de linha no caso escalar, não tem saída: Tem que calcular pelo método direto! Mas não se preocupe, pois, o método não é complicado, você se lembra?!
A gente sempre deve começar entendendo melhor sobre a nossa curva e encontrando uma parametrização que salve nossa vida. Vem comigo!
A nossa curva está sobre , então a gente pode usar uma parametrização explícita da forma:
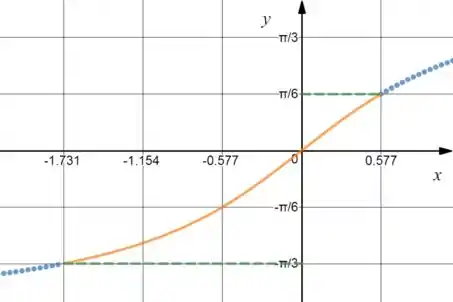
Pra facilitar a visualização eu botei o em escalas de e o em escalas de ;)
Passo 2
Vamos encontrar agora o nosso termo . Não se esqueça que é dado por
Derivando a nossa parametrização, obteremos
Logo
Passo 3
Lembre-se que integrais de linha vai se transformar em uma integral simples de uma variável, logo a gente tem que eliminar aquele da nossa função.
A gente faz isso aplicando a nossa função em cima da nossa parametrização, lembrou?!
Passo 4
Montando a nossa integral...
Note que não coloquei os limites de variação de ainda apenas para facilitar nas contas dessa integral. Em falar nisso, bora lá?
Bom, vamos começar escrevendo tudo em função de senos e cossenos? É bem mais confortável trabalhar com eles né? Se liga:
Fazendo essa substituição aqui:
Chegamos no seguinte:
Opa beleza! Viu a substituição que dá pra fazer agora? Se liga:
Aí ficamos com:
Agora é só a gente substituir de volta pra variável !
Passo 5
Pra finalizar é só substituir os limites de integração!