IME, Cálculo 2, 2020, VE1, Q2
Uma partícula se move a o longo da parábola de tal forma que as componentes vertical e horizontal do vetor aceleração são sempre iguais. Se a partícula gasta 90s para ir do ponto à origem dos eixos, quanto tempo a mesma levará para ir do ponto P ao ponto ?
Passo 1
Fala, pessoal. O gatilho dessa questão é perceber que a aceleração varia de direção e módulo de forma a compensar e conseguirmos impor a condição do enunciado e ainda que a velocidade é proporcional a derivada da curva a qual é tangente a esta:
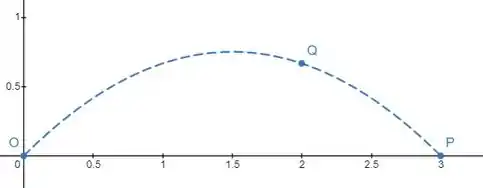
Assim, sendo a curva dada por:
Agora, teremos que a velocidade da partícula é dada por:
Onde é escalar. Ainda:
Agora vai!
Igualando as componentes da aceleração:
Logo,
Agora, nossas velocidade e aceleração estão definidas a menos dessa constante D, pois .
Passo 2
Para calcular tempo de percurso utilizamos a integral de linha até o ponto de chegada :
Onde é o parâmetro de , isto é, . Assim, com , temos:
Repare pois que , logo para a coordenada x de chegada. Assim, para , temos e:
Passo 3
Por fim, observe que se , temos de forma que:
Resposta
A partícula leva 50s para chegar a .