Integrais de linha – caso escalar
Considere a curva plana parametrizada por
- Faça um esboço da imagem/ traço de .
- Calcule a integral, com respeito ao comprimento do arco, da função escalar ao longo da curva parametrizada .
Passo 1
Letra a)
Se a gente olhar para a parametrização da curva , percebemos que:
Ou seja, essa parametrização é de uma elipse (em coordenadas elípticas).Como , temos meia volta. Comparando a equação acima com a equação geral de um elipse:
Temos os coeficientes e , os raios menor e maior, respectivamente, da elipse. Levando isso para o desenho:
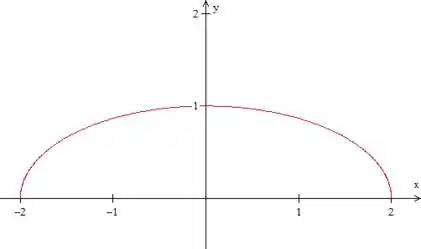
Passo 2
Letra b)
Já que a curva já nos foi dada parametrizada, a primeira coisa a fazer aqui é derivar essa parametrização:
Passo 3
Agora, calculamos :
Passo 4
Podemos, então, substituir na fórmula abaixo, escrevendo em função de , nosso parâmetro:
Escrevendo o campo nas variáveis da parametrização, temos:
Então a integral fica
Passo 5
Agora falta resolver a integral né? Vamos fazer a substituição
Levando para a integral, temos:
Resposta
- 0