Integrais de linha – caso escalar
Calcule a integral de linha escalar , sendo a curva em dada por ligando os pontos e pelo arco de menor comprimento.
Passo 1
Vamos buscar uma parametrização para a curva , uma elipse dada por:
Podemos, então, representar essa curva por . O arco de menor comprimento é aquele que vai de até pelo sentido anti-horário, como você pode ver na figura:
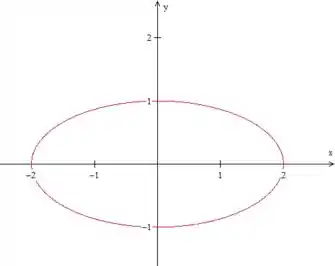
Temos, então, .
Passo 2
Vamos, agora, calcular :
Passo 3
Agora, calculamos :
Passo 4
Podemos, então, substituir na fórmula abaixo, escrevendo em função de :
Passo 5
Agora vamos chamar , temos .
A integral passa a ser:
Resposta
Exercícios de Livros Relacionados
Calcule a integral de linha, onde C é a curva dada. ∫ C x + 2 y d x + x 2 d y C consiste nos segmentos de reta de ( 0,0 ) a ( 2,1 ) e de ( 2,1 ) a ( 3,0 ) .
Calcule o valor da integral de linha, onde C é a metade é a metade do círculo x 2 + y 2 = 16
Calcule a integral de linha, onde C é a curva dada.int_C x y^3 d s , C : x = 4 s e n t , y = 4 cos t , z = 3 t , 0 = t = (pi)/(2)
Determine o valor exato de ∫ C x 3 y 5d s , onde C é a parte da astróide x = c o s 3 t , y = s e n 3 t no primeiro quadrante.
Calcule a integral de linha, onde C é a curva dada.int_C x y^4 d s , C é a m e t a d e d i r e i t a d o c í r c u l o x^2 + y^2 = 16 é í