Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução aos Limites de Funções de Várias Variáveis

Ver Teoria
Exercício 441234567891011121314151617181920212223242526272829303132333435363738394041424345464748495051525354

Enunciado

UNICAMP – Cálculo 2 – Provas Antigas – P1 – 2021.2 - 5ª Tarde – Questão 1a

  1. Determine se o limite

lim x , y → ( 0,0 ) ⁡ x y 2 x 3 - y 2

Existe ou não. Se existir, calcule seu valor.

Passo 1

Eaeeee, belezinha??? Seguinte... a questão nos pede o limite de duas variáveis que tendem a zero!! Ou se preferir, o limite de um ponto no plano cartesiano que tende à origem!

Mas se a gente só substituir x = 0 e y = 0 , teremos uma indeterminação do tipo 0 0 , concorda? Pois é...

Mas e aí??? Como resolvemos isso?

Vamos relembrar que podemos substituir coordenadas no plano cartesiano por coordenadas polares da seguinte forma:

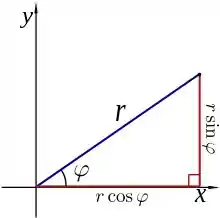
Assim podemos fazer x = r cos ⁡ ϕ e y = r sin ⁡ ϕ .

Passo 2

Tá... mas no que isso ajuda?

Vem cá, vamos pensar juntos... Se queremos que o ponto ( x , y ) tenda a zero, então é a mesma coisa dizer que queremos que r tenda a zero, né?!

Assim, baseado nessa informação, podemos reescrever o limite da seguinte forma:

lim x , y → ( 0,0 ) ⁡ x y 2 x 3 - y 2 = lim r → 0 ⁡ r cos ⁡ ϕ ∙ r 2 sin 2 ⁡ ϕ r 3 cos 3 ⁡ ϕ - r 2 sin 2 ⁡ ϕ

Agora vamos desenvolver!!!

Passo 3

Desenvolvendo a equação, temos:

lim r → 0 ⁡ r cos ⁡ ϕ ∙ r 2 sin 2 ⁡ ϕ r 3 cos 3 ⁡ ϕ - r 2 sin 2 ⁡ ϕ =   lim r → 0 ⁡ r 3 cos ⁡ ϕ sin 2 ⁡ ϕ r 3 cos 3 ⁡ ϕ - r 2 sin 2 ⁡ ϕ

= lim r → 0 ⁡ r cos ⁡ ϕ   sin 2 ⁡ ϕ r cos 3 ⁡ ϕ - sin 2 ⁡ ϕ

= 0 ∙ cos ⁡ ϕ   sin 2 ⁡ ϕ 0 ∙ cos 3 ⁡ ϕ - sin 2 ⁡ ϕ

= 0 - sin 2 ⁡ ϕ

= 0

Entendeu direitinho? Responde aee ;)

Resposta

lim x , y → ( 0,0 ) ⁡ x y 2 x 3 - y 2 = 0

Exercícios de Livros Relacionados

Dado (x_0 , y_0) in R^2 , mostrar que underset([[x - x_0],[y - y_0]])(lim) y = y_0 .
Usando a definição de limite, mostre que:e) underset([[x - 0],[y - 0]])(lim) (x y^3)/(x^2 + y^2) = 0
Usando a definição de limite, mostrar que:underset([[x - - 1],[y - 2]])(lim) (5 x - 2 y) = - 9
Usando a definição de limite, mostrar que:underset((x , y) - ( 2,3 ))(lim) (3 x + 2 y) = 12
Utilize uma tabela de valores numéricos de f x ,y para x ,y perto da origem para conjecturar sobre o limite de f x ,y quando x ,y → 0 ,0 . Em seguida, explique por que sua conjectura está correta. f x