Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade Angular e Aceleração Angular Instantâneas

Ver Teoria
Exercício 4412345678910111213141516171819202122232425262728293031323334353637383940414243454647484950515253545556

Enunciado

USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 42b

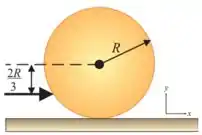
42. Uma bola de bilhar de raio R e massa M , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância 2 R / 3 abaixo da linha horizontal do centro. A velocidade linear da bola é v 0 .

(b) Qual a velocidade da bola uma vez iniciado o rolamento sem escorregamento?

Passo 1

Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse problema temos uma bola de massa M e raio R parada em uma mesa. Ela recebe um impacto horizontal a uma distância h = 2 R / 3 abaixo do seu centro com a bola adquirindo uma velocidade v 0 e uma rotação.

Com isso queremos descobrir qual é a velocidade linear da bola após parar de deslizar sobre a superfície.

Lembra como fazemos isso? 👀

Anteriormente calculamos que a velocidade angular inicial da bolinha após o impacto é dada por

ω 0 = - 5 v 0 3 R

Para descobrir a velocidade linear da bola, temos que aplicar a equação do movimento uniformemente variado

v = v 0 + a t

Mas pra isso, temos que encontrar a e t a partir das equações que já sabemos e das informações dadas...

Bora começar! 😬

Passo 2

Aplicando a segunda lei de Newton no instante após o impacto, vemos que o torque gerado pela força de atrito é dado por

τ = F a t R

Sabemos que a força de atrito é dada por

F a t = μ c N = μ c M g

E também sabemos que o torque pode ser calculado como

τ = I α

Ou seja, como I da esfera é dada por I = 2 M R 2 5

F a t R = 2 M R 2 5 α

μ c M g R = 2 M R 2 5 α

Simplificando...

μ c g = 2 R 5 α

Logo, encontramos que a aceleração angular é dada por

α = 5 μ c g 2 R

Tranquilo até aqui? 🤔

Passo 3

Para descobrir a aceleração linear, aplicamos a segunda lei de Newton novamente e vemos que

F a t = - M a → μ c M g = - M a

a = - μ c g

Já encontramos a aceleração, falta encontrarmos o tempo que leva até parar de deslizar...

Pra isso, podemos relacionar as equações do movimento retilíneo uniformemente variado e do movimento circular uniformemente variado...

v = v 0 + a t

ω = ω 0 + α t

Como ω = v R , então a segunda equação pode ser escrita como

ω = v R = ω 0 + α t

v = ω 0 + α t R

Igualando as duas equações de v , temos

v 0 + a t = ω 0 + α t R

Substituindo α , a e ω 0 ...

v 0 + - μ c g t = - 5 v 0 3 R + 5 μ c g 2 R t R

v 0 - μ c g t = - 5 v 0 3 + 5 μ c g 2 t

Isolando t

5 μ c g 2 t + μ c g t = v 0 + 5 v 0 3

7 μ c g 2 t = 8 v 0 3

t = 16 v 0 21 μ c g

Bacana, não é? 😁

Passo 4

Agora que encontramos a e t , podemos substituir na equação do movimento retilíneo e obter a velocidade linear no instante que estamos interessados

v = v 0 + a t

v = v 0 - μ c g 16 v 0 21 μ c g

Simplificando...

v = v 0 - 16 v 0 21

v = 5 v 0 21

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

v = 5 v 0 21

Exercícios de Livros Relacionados

A posição angular de um ponto de uma roda é dada por θ=2,0+4,0 t 2+2,0 t 3 , onde θ está em radianos e t em segundos. Em t= 0 , qual é (a) a posição e (b) a velocidade angular do ponto? (c) Qual éa ve
Um disco com raio igual a 25,0c m está livre para girar em torno de um eixo perpendicular a ele e que passa pelo seu centro. Ele possui um fio delgado, porém forte, enrolado em torno da sua borda e o
Um bom lançador de beisebol pode arremessar uma bola a 85 m i / h com uma rotação de 1800r e v / m i n . Quantas revoluções a bola realiza até chegar à base principal? Para simplificar, suponha que a
Uma polia com 8,0c m de diâmetro tem uma corda de 5,6m de comprimento enrolada na borda. Partindo do repouso, a roldana recebe uma aceleração angular constante de 1,5r a d / s 2 , (a) que ângulo a rol
Quando uma torrada com manteiga é deixada cair de uma mesa, adquire um movimento de rotação. Supondo que a distância da mesa ao chão é 76c m e que a torrada não descreve uma revolução completa, determ