UFSCAR – Sem Campus – Física 1 – SUB –2021.2 – Prof. Raphael Santarelli – Questão 4b
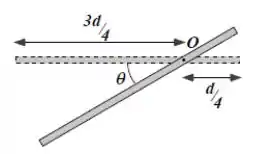
Uma haste metálica fina, de comprimento e massa , pode girar em torno de um eixo horizontal que a atravessa perpendicularmente (saindo da página), à distância de sua extremidade (ver figura ao lado). A haste é solta a partir do repouso de sua posição horizontal. Calcule:
b) As velocidades lineares do centro de massa e das extremidades da barra quando
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma haste que pode girar em torno de um eixo horizontal situado à distância de sua extremidade.
A questão nos pede para descobrirmos as velocidades lineares do centro de massa e das extremidades da barra quando ela é solta a partir do repouso fazendo um ângulo .
E aí? Bora lá?
Passo 2
Bom... considerando que a relação entre as velocidades linear e angular é dada por , e usando a expressão obtida para a velocidade anteriormente podemos encontrar as velocidades.
Assim, a velocidade no centro de massa é dada por:
Passo 3
Agora, a velocidade da extremidade mais próxima do eixo:
E a velocidade mais distante do eixo:
Entendeu direitinho? Responde aee ;)
