UNB – Sem Campus – Física 1 – Lista – Listas de Exercício Física 1 – UnB – Lista 12 – Dinâmica do Movimento - Questão 4 – Alternativa a)
Um fio é enrolado diversas vezes em torno da periferia de um pequeno aro de raio e de massa . A extremidade livre do fio é mantida fica e o aro é liberado a partir do repouso (figura abaixo). Após o aro cair por , calcule
a velocidade escalar angular do aro em rotação
Passo 1
Eaew, belezinha?
Que problema assustador neh? Eu posso te dizer, que dependendo do caminho que seguir, isso aqui pode ser extremamente complicado, como pode ser extremamente simples! Vamos tentar seguir pelo segundo! Ahahahah! A situação descrita no enunciado é como um ioiô desenrolando (Mas sem o vai e volta). Quando o fio desenrola, o aro desce até uma altura mais baixa, enquanto desce, esse aro gira ganhando uma velocidade angular. Note só que legal, um objeto caiu uma altura e ganhou uma velocidade! Isso está implorando para ser tratado através de conservação de energia! Então vamos tentar ir por aí!
Passo 2
Primeira coisa! Vamos estabelecer um referencial para resolver nosso problema! Ele fica da seguinte forma
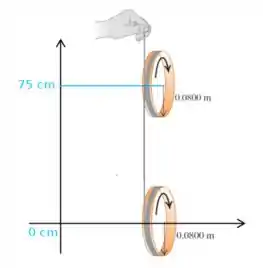
Ou seja, o aro começa em uma altura e desce até a origem do sistema de coordenadas! O aro parte do repouso, então temos que na altura inicial, podemos escrever
Já que sem velocidade, não temos energia cinética! Já nesta escolha de referencial, temos que na origem
Já que podemos simplesmente escolher um referencial em que . Igualando ambas as expressões, nós podemos dizer que
Parece abstrato, mas nosso problema está resolvido! Sabe me dizer porquê? Vem comigo!
Passo 3
De cara temos que a energia potencial é dada por
Essa é a mesma fórmula desde sempre quando estávamos aprendendo o B+A=BA no ensino médio. Agora, no entanto, é um pouquinho mais complicado. Como este é um corpo rígido, temos que a energia cinética é dada por dois termos
Encontrar ambos estes componentes é a nossa próxima tarefa! Bora lá!
Passo 4
Primeiro, a energia cinética de translação é dada para um corpo rígido calculando
Em que é a velocidade do centro de massa, calculada como
Aqui é conveniente escrever em termos da velocidade angular . De forma que a nossa energia cinética de translação é
Belezinha! Vamos calcular a outra energia cinética agora! Vem comigo!
Passo 5
A energia cinética de rotação de um corpo rígido pode ser calculada utilizando
Em que é o momento de inércia do corpo em rotação. Em nosso caso, temos um aro, e é dado por
Ou seja, substituindo em nossa energia cinética, nós obtemos
Maaaaravilha! Temos ambas as energias! Agora é só somar tudo!
Passo 6
Somando e temos que que
E, utilizando a conservação da energia mecânica total, temos que
Portanto, substituindo o que calculamos ao longo dos passos, temos
Podemos finalmente isolar a nossa velocidade angular! Obtendo
Só precisamos jogar alguns valores! E uff... deu bom! Bora lá!
Passo 7
Primeiro, se tirarmos a raiz, e escolhermos o sinal positivo (Isso é só uma escolha se o aro está girando no sentido anti-horário ou horário), temos
Que, jogando na calculadora, nos dá
Beeelezura! Aí está a nossa alternativa Bora fazer a segunda alternativa agora! Até daqui a pouco!