Uma partícula executa o movimento espiral mostrado na figura com e onde , e são constantes positivas. Marque a opção correta abaixo que descreve o movimento quando :
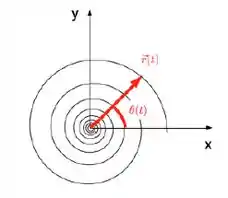
(a) Aceleração radial e a velocidade radial decrescem exponencialmente.
(b) Aceleração radial é nula enquanto a velocidade radial é nula.
(c) Aceleração radial cresce exponencialmente enquanto a velocidade radial decresce linearmente no tempo.
(d) Aceleração radial e a velocidade radial crescem exponencialmente.
(e) Aceleração radial é nula enquanto a velocidade radial cresce exponencialmente.
Passo 1
Bom, temos uma partícula realizando um movimento em espiral.
Hum, essa questão não está cheirando bem...

Calma, hahah. Não precisa ficar tão desconfiado.
Mas como a gente descreve esse movimento espiralar?
Se pensarmos num vetor unitário radial que gire junto com a partícula, apontando em sua direção:
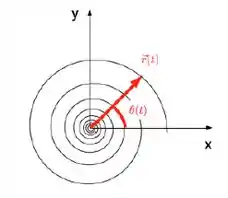
Podemos descrever esse movimento como um vetor (vetor posição), em que o módulo já foi dado pelo enunciado e a direção desse vetor será em :
A questão toda se baseia em achar a velocidade e a aceleração radial desse movimento.
Se temos o vetor posição , podemos derivar esse cara e achar o vetor velocidade :
E se temos o vetor velocidade , podemos derivar esse cara e achar o vetor aceleração :
Massssss, temos que tomar muito cuidado na hora de derivar esse vetor, pois não podemos simplesmente derivar o módulo de .
A grande diferença desse vetor unitário (direção de do vetor ) para os vetores unitários (direção do eixo ) e (direção do eixo ), é que dentro do referencial de eixos , esse vetor vai variar no tempo, já que ele está constantemente mudando de direção:
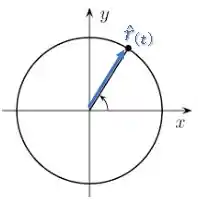
E se não é uma constante e sim um termo que varia no tempo, agora existe um produto de dois termos que variam no tempo, o primeiro e o segundo ). Logo existe uma regra do produto nessa derivada.
Passo 2
Lembrando a regra do produto para uma derivada...
Se temos dois termos que variam e estamos derivando o produto desses termos, temos:
Ou seja, derivamos o primeiro e mantemos o segundo e depois mantemos o primeiro e derivamos o segundo.
Passo 3
Então, aplicando a regra do produto naquela derivada, temos:
Lembrando que é um termo constante, portanto não entra na regra do produto.
Agora, vamos fazer derivar separadamente esse termo para não complicar muito essa linha de desenvolvimento.
Passo 4
Segura na minha mão e vem comigo.

Para derivar esse vetor unitário , vamos escrevê-lo em coordenadas cartesianas.
Sua componente em será um termo dado pelo cosseno, em será um termo dado pelo seno e sua velocidade angular dada no enunciado é :
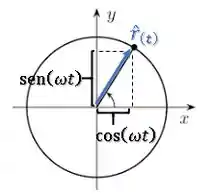
Esse vetor pode ser escrito como:
Essa é a direção radial.
Vamos aproveitar e definir também um vetor perpendicular, que chamaremos de .
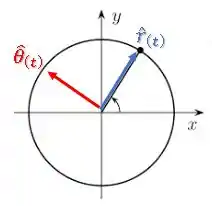
Essa será a direção tangencial ao movimento da partícula:
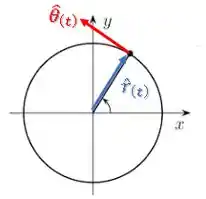
Sua expressão em coordenadas cartesianas é:
Passo 5
Agora, vamos derivar esses dois caras, pois vamos precisar disso no nosso desenvolvimento.
Começando com :
Tanto o termo “” quanto o termo “” vão precisar da regra da cadeia para a expressão de dentro da função e :
Colocando em evidência o , temos que aparece exatamente o vetor unitário :
Agora vamos derivar o :
Se, novamente, colocarmos em evidência o termo , podemos ver que aparece exatamente o vetor unitário :
Então, vemos que esses vetores unitários se relacionam quando são derivados, o que vai ser útil na hora de desenvolver o nosso problema.
Passo 6
Agora, depois desse rolê todo, vamos finalmente voltar para a nossa questão.
Vamos derivar o vetor posição , achando o vetor velocidade :
Derivando o termo , temos que a derivada de uma exponencial se matém a mesma, porém temos uma regra da cadeia:
E derivando o termo , acabamos de ver no Passo 5 que achamos:
Substituindo esses termos, ficamos com:
Esse é o vetor velocidade, e podemos ver que o termo na direção de é a velocidade radial enquanto o termo na direção de é a velocidade tangencial.
Ou seja, a velocidade radial da partícula é dada por:
Portanto, já descobrimos que essa velocidade cresce exponencialmente.
Mas queremos o vetor aceleração também, então devemos derivar novamente.
Passo 7
Derivando o vetor , vamos aplicar agora duas vezes a regra do produto.
Para o primeiro termo da soma, a regra do produto fica:
Lembrando que os termos e são constantes e por isso não entram na regra do produto. Continuando, vamos usar novamente a derivada de que já calculamos:
Aplicando a distributiva, temos:
Beleza!
Agora, vamos aplicar a regra do produto para o segundo termo, usando as mesmas estratégias:
Fazendo a distributiva, temos:
Substituindo os dois termos na expressão de :

Tá no final, eu prometo!
Passo 8
Eu sei que a expressão da aceleração está meio bizonha...
Mas como queremos tirar alguma conclusão sobre a aceleração radial , vamos agrupar todos os termos em cada uma das direções.
A expressão era essa.
Tanto o primeiro termo quanto o quarto termo estão em , então:
Podemos ainda colocar “” em evidência e somar os termos da nova segunda parte:
Ufaaaaa, chegamos em alguma expressão minimamente mais tranquila...
Passo 9
Agora, o que podemos concluir sobre esse vetor aceleração?
O termo multiplicando é a aceleração na direção radial, enquanto o termo é a aceleração na direção tangencial:
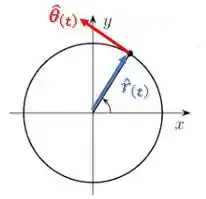
Como o enunciado nos deu que:
Temos que:
Ou seja, o termo de aceleração radial zera para essa condição, enquanto o termo de aceleração tangencial é apresenta um valor positivo e exponencial crescente.
Logo, ficamos com a letra (e).

Foi sofrida, mas sobrevivemos ahaha.
Resposta
Letra (e)