A peça de uma máquina tem o formato de uma esfera maciça e uniforme com massa de e o diâmetro de . Ela está girando em torno de um eixo com atrito desprezível que passa pelo seu centro, mas em um ponto no seu equador ela está roçando contra uma parte metálica, resultando em uma força de atrito de neste ponto.
Ache a aceleração angular.
Passo 1
Eaew, firme e forte?
Antes de qualquer coisa! Vamos tentar visualizar este problema! Imagine uma esfera rotacionando e raspando bem pouquinho em uma parede (aproximação para que isso ocorra apenas em um ponto tangencial), o esquema é o seguinte
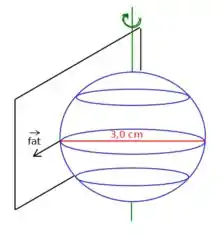
O enunciado nos dá que , e é devido a esta única força gerando um torque sobre a esfera, que temos uma aceleração angular! Bem parecido com uma aceleração linear sendo causada por uma força (Segunda lei de Newton!), não é? Isso é chamado de Segunda Lei de Newton para rotações e é dada algebricamente como
Em que é o momento de inércia de nossa esfera e é a aceleração angular que queremos calcular, e por último é o torque resultante sobre a esfera! Consegue utilizar estas informações? Segue comigo se estiver com dificuldades!
Passo 2
A primeira coisa é notar que temos apenas uma força atuando sobre o sistema, que é a força de atrito , portanto, nosso torque resultante é dado apenas pela ação desta força em desacelerar o giro da esfera. Ou seja, temos que
Neste caso é mais simples analisarmos a expressão acima em termos do módulo, lembrando que
Vamos utilizar isso para calcular o nosso torque e então a nossa aceleração! Bora Bora!
Passo 3
Primeira coisa a se notar é que é a distância do centro da esfera até o ponto que rela na parede, e portanto, seu módulo é o raio da esfera, e o vetor é perpendicular a força de atrito, e assim temos que
E, também que
De forma que podemos calcular a intensidade do nosso torque como
Mas e daí neh? O que eu faço com isso? Eu tenho que este torque causa uma desaceleração, o que pode ser estimado com a segunda lei de newton da rotação! Vamos fazer isso agora!
Passo 4
Repetindo aqui a segunda lei da rotação, temos
Nós calculamos no último passo que . E, para uma esfera que gira em torno do seu centro temos que
Em que e . Calculando o momentum de inércia da esfera, temos
Agora parece que temos tudo que faltava certo? Falta só calcular!!
Passo 5
Pegando o módulo do nosso torque resultante, obtemos
E, isolando a aceleração, temos
Ou, jogando tudo em uma calculadora, podemos obter
E só por completeza, como a esfera gira em torno do eixo , temos que o torque está nesta direção, mas como ele causa uma desaceleração, temos que o vetor aceleração angular é tal que
Essa foi a primeira alternativa! Bora para a próxima! Te vejo jajá!