UnB - Listas - Física 1 - Lista 3 Vetores - Questão 4
Um avião sai do aeroporto em Galisteo e voa a e, em seguida, muda de direção para voar , após o qual faz um pouso de emergência em um pasto. Quando o aeroporto envia uma equipe de resgate, em que direção e a que distância esta tripulação deve voar para ir diretamente a este avião?
Passo 1
Fala aí, beleza?? Vamos para mais uma questãozinha!
Vamos desenhar a situação que o enunciado descreve para podermos visualizar melhor o problema.
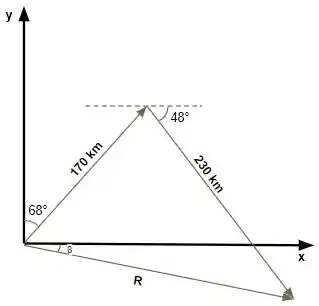
Então a questão nos fala que um avião saiu do aeroporto e voou cerca de formando um ângulo de com o eixo y (norte). E em seguida, muda a direção voando cerca de em um ângulo de com o eixo x (leste) e faz um pouso de emergência.
Portanto, temos que encontrar a o módulo da distância e a direção que a equipe de resgate deve seguir para encontrar esse avião. E aí, o que devemos fazer primeiro??
Passo 2
Vamos começar decompondo as distâncias em relação ao eixo x:
Dica: quando estamos resolvendo questões sobre vetores é ideal começarmos primeiro decompondo as forças, distâncias… em relação aos eixos.
Agora vamos decompor as distâncias em relação ao eixo y:
Alerta!!!Aqui não podemos esquecer que a componente será negativa uma vez que aponta no sentido -y.
Passo 3
Agora para encontrarmos as componentes da distância basta que utilizemos o teorema de pitágoras, uma vez que as componentes do vetor sempre formam um triângulo retângulo com o mesmo.
Então uma parte da questão foi resolvida! Ainda falta a outra…
Passo 4
Ainda falta encontrarmos o que???
Temos que encontrar a direção em que o resgate deve seguir e como fazemos isso?
Temos que utilizar a tangente , já que sofremos para encontrar as componentes, nada mais justo que utilizar novamente aqueles valores, né? Vem comigo…
Tá mas precisamos do ângulo né, então vamos utilizar a função arco-tangente para descobrir isso e finalizar nosso probleminha:
Terminamossss! Viu como vocês são incríveis? Conseguimos chegar até aqui juntos :)
Beijinhos e até mais!!!!!!