Determine o módulo, a direção e o sentido dos vetores representados pelos seguintes pares de componentes:
Passo 1
Cada par de vetores vai formar uma resultante e o módulo dessa resultante é retirado a partir das componentes, é o que faremos para todos os itens, sem mistério.
Para calcular o módulo a partir das componentes vamos utilizar a seguinte fórmula:
Para saber o sentido e a direção do vetor, temos que prestar muita atenção aos sinais das camponentes e saber que:
Passo 2
a)
Substituindo os valores:
Vamos fazer um desenho desse vetor, colocando um sistema de eixos e suas componentes no plano cartesiano.
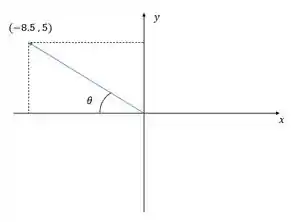
Agora vamos calcular o ângulo e avaliar se está coerente.
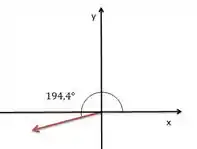
Como a componente x é negativa e a componente y é positiva, o vetor está no segundo quadrante, como no desenho.
O ângulo do que o vetor faz deve ser calculado a partir do primeiro quadrante portanto vamos guardar o valor de em módulo e retirar de como podemos ver na figura.
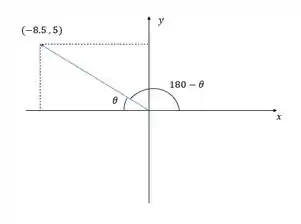
Pro calculo do ângulo da posição usaremos o módulo de
Mas não se esqueça de tirar esse ângulo dos 180 para ter a posição do vetor:
Passo 3
b)
Substituindo os valores:
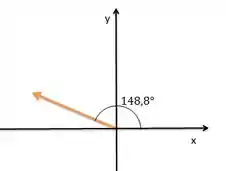
Vamos de novo fazer um desenho, aqui poderemos representar somente os sinais pra avaliar a coerência do ângulo encontrado.
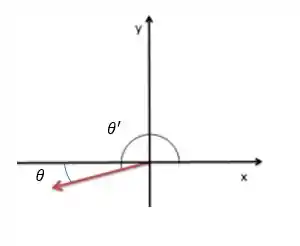
Vamos calcular o valor de , começando pela sua tangente.
Também usaremos o módulo ainda que pro caso positivo não faça diferença alguma:
Como a componente negativa e a componente é negativa, o vetor esta no terceiro quadrante. Nesse caso o ângulo que o vetor faz com o primeiro quadrante é:
Passo 4
c)
Substituindo os valores:
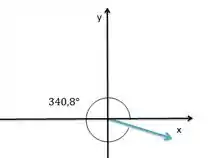
Vamos avaliar na figura a posição do vetor e o seu ângulo:
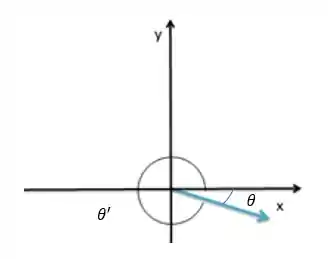
Calculando o valor de
Como a componente x é positiva e a componente y é negativa, o vetor esta no quarto quadrante.
Nesse caso calculamos o ângulo
E subtraímos de o seu módulo:
Logo:
Resposta