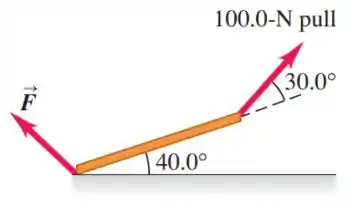
Dizemos que um objeto está em equilíbrio se todas as forças atuando nele estiverem balanceadas (somam zero). A figura abaixo mostra uma viga pesando que é apoiada em equilíbrio por um puxão de e uma força no chão. A terceira força na viga é o peso de que age verticalmente para baixo. (a) Use os componentes do vetor para encontrar a magnitude e a direção de . (b) Verifique a razoabilidade de sua resposta na parte (a) fazendo uma solução gráfica aproximadamente em escala.
Passo 1
Bom dia, boa tarde, boa noiteeee gente linda!! Se tá difícil por aí, deixa que a gente te ajuda. Vamos resolver mais uma com muito ânimo e carinho? Bora lá!!
Um corpo se encontra em equilíbrio quando todas as forças que agem sobre esse corpo estiverem balanceadas, ou seja, a soma vetorial dessas forças deve ser igual a zero. Sabendo disso, a questão nos fala que existe um objeto que está em equilíbrio e nesse objeto atuam forças: Força Peso(), Força de um Puxão() e Força .
Devemos então encontrar a magnitude(valor) e a direção (ângulo) em que se encontra a Força . E aí, meus amores sabem por onde começar??? Vamos juntos!
Passo 2
Vamos começar escrevendo o fato de que se o corpo em questão está em equilíbrio é porque a soma vetorial das forças que atuam nele se anulam.
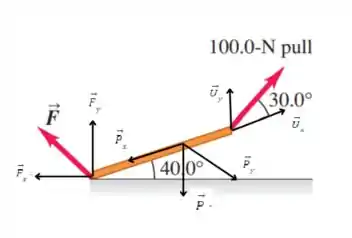
E como estamos trabalhando com vetores é sempre muito importante analisarmos as componentes de cada força. Assim, vamos decompor as forças em relação ao eixo x:
Note que a Força Peso atua diretamente para baixo, entretanto, o objeto está inclinado e isso significa que essa força também estará produzindo componentes horizontais e verticais!!!
Passo 3
Vamos repetir o passo anterior só que agora em relação ao eixo :
Excelente! Já temos as componentes da Força , agora só falta descobrir a sua magnitude

Calmaaaa! Essa é a parte boa, encontrar a magnitude de um vetor significa que temos que apenas utilizar o Teorema de Pitágoras tendo em vista que o vetor e suas respectivas componentes formam um triângulo retângulo.
Tudo bem até aqui?!
Seguimos então!
Passo 4
Agora falta encontrar a direção, ou melhor, o ângulo em que se encontra o vetor em relação ao eixo x.
É importante que você esteja craque nessas relações básicas da trigonometria se não o seu cérebro vai dar um nó nesse tipo de questão hahaha
Como já temos o valor de cada componente, vamos utilizar aqui a função tangente. Sendo assim,
E agora? Como vamos chegar no ângulo?

Vamos utilizar a função inversa da tangente para descobrir o valor do ângulo em questão.
E como a componente x da nossa Força é negativa e a componente y é positiva, podemos afirmar que a nossa força se encontra no segundo quadrante. Logo,
em relação ao eixo x
Ao se somar as forças horizontais e verticais obtém-se um “cancelamento” o que indica que as forças estão se compensando em ambas as direções. Assim, é perceptível que o sistema realmente está em equilíbrio.
Show de bolinhas?! Vocês mandam muito bem!
Continuem treinando :)
Resposta
Magnitude :
Direção: em relação ao eixo x