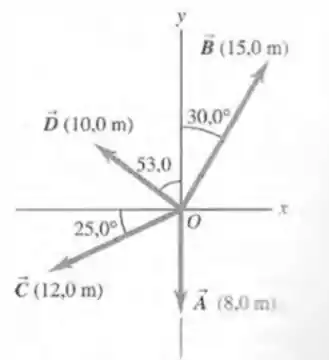
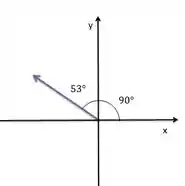
Escreva cada vetor indicado na figura abaixo em termos de vetores unitários .
Passo 1
Para calcular cada componente vamos precisar saber o módulo de cada vetor e a o ângulo que o vetor faz com o eixo
Passo 2
Considerando o ângulo com o eixo temos:
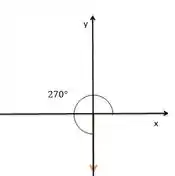
Passo 3
Como o ângulo com o eixo vale , o ângulo com o eixo vale
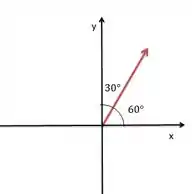
Assim temos:
Passo 4
Como o ângulo com o eixo val e o ângulo está abaixo do eixo, temos que o ângulo com eixo vale
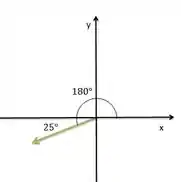
Assim temos:
Passo 5
O ângulo com o eixo vale
Assim temos:
Resposta
Exercícios de Livros Relacionados
Um explorador polar foi surpreendido por urna nevasca, que reduziu a visibilidade a praticamente zero, quando retornava ao acampamento. Para chegar ao acampamento, deveria ter caminhado 5,6k m para o
Em um jogo de xadrez ao ar livre, no qual as peças ocupam o centro de quadrados com 1,00m de lado, um cavalo é movido da seguinte forma: (1) dois quadrados para a frente e um quadrado para a direita;
Um vetor deslocamento r → no plano x y tem 15m de comprimento e faz um ângulo θ = 30 ° com o semieixo x positivo, como mostra a Fig 3-26. Determine (a) a componente x e (b) a componente y do vetor.
Quais são (a) a componente x e (b) a componente y de um vetor a → do plano x y que faz um ângulo de 250 ° no sentido anti-horário com o semieixo x positivo e tem um módulo de 7,3m ?
Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano x y . As componentes ( x e y ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: 30,0