UnB - Listas - Física 1 - Lista 3 Vetores - Questão 5b
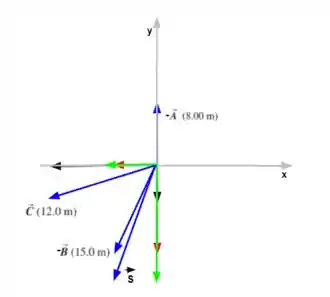
Encontre a magnitude e a direção do vetor . Em um diagrama, mostre como é formado a partir desses vetores.
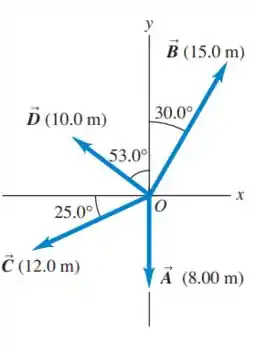
Passo 1
E aii, galerinha!! Como estão? Vamos juntos pra mais uma!!
Primeiro vamos esclarecer que é a mesma coisa que , o vai indicar apenas que o vetor estará no sentido contrário.
Então temos que encontrar o vetor resultante que representa a soma dos vetores e em seguida devemos representar como esse vetor é formado a partir dos outros vetores. Por onde começar???
Vamos começar projetando os vetores sobre os eixos, ou melhor, decompondo esses vetores.
Assim, vamos começar decompondo os vetores em relação ao eixo :
Detalhe, observem que o vetor está totalmente sobre o eixo não tendo assim componente sobre o eixo x. E além disso, lembrem se a componente apontar para os eixos negativos o sinal de terá de ser acrescentado.
Passo 2
Agora faremos a decomposição para o eixo y:
Passo 3
Como já encontramos as componentes de agora para achar de fato a sua magnitude basta aplicarmos o teorema de Pitágoras já que as componentes de um vetor formam com o mesmo um triângulo retângulo.
Passo 4
Agoraaaaa só falta encontrar a direção, em outras palavras, o ângulo em que esse vetor se encontra em relação à vertical.
Podemos fazer isso utilizando a função tangente já que nos passos anteriores encontramos as componentes e vimos que essas formam um triângulo entre si.
Como estamos interessados no ângulo em si e não na tangente, então vamos solucionar esse problema usando a função arco-tangente.
em relação ao eixo
Ainda falta um detalhe para finalizarmossss
Passo 5
Vamos representar todas as componentes dos vetores que geram o vetor .
Vemos que o em relação ao há apenas uma variação de sentido, sendo assim, o ângulo e a magnitude do vetor oposto continuaontínua sendo a mesma. E isso se aplica aos demais vetores opostos.
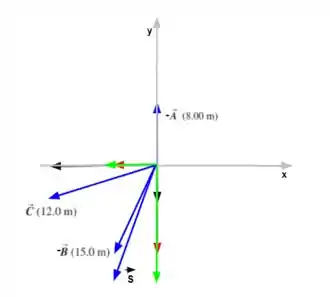
Os vetores em preto representam as componentes do vetor , já os vetores em vermelho representam as componentes do vetor e por fim, temos os vetores em verde representando as componentes do vetor resultante .
É isso xuxus, concluímos com sucesso!
Bora terminar essa lista de vetores?! 😊
Resposta
em relação ao eixo -y
