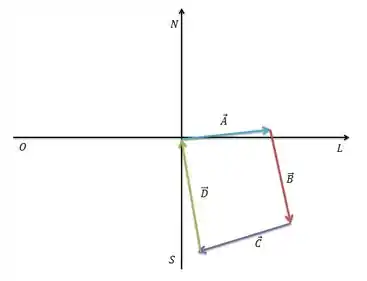
Em um vôo de treinamento, uma aprendiz de piloto voa de Lincoln, no Estado de Nebraska, até Clarinda, no Iowa; a seguir até St. Joseph, no Missouri: depois até Manhattan, no Kansas, como na figurinha abaixo. Os ângulos formados pelos deslocamentos são medidos em relação ao norte: significa sentido sul para o norte, é o leste, é o sul e é o oeste. Use o método dos componentes para achar:
- A distância que ela terá de voar para voltar para Lincoln
- A direção (em relação ao norte) que ela deverá voar para voltar ao ponto de partida. Ilustre a solução fazendo um diagrama vetorial.

Passo 1
Nesse exercício, além de dar aquele rolé pelos Estados Unidos, vamos trabalhar com deslocamentos. Se lembra, laaaaa na teoria, dos carrinhos? Então, como deslocamentos são vetores e no final ele quer voltar para o mesmo ponto, temos que deslocamento total é zero, ou seja, a soma vetorial precisa ser zero.
Passo 2
Alternativa a)
Como o deslocamento total é zero, temos:
Onde:
Passo 3
Agora vamos analisar componente por componente, começando pela componente para o leste (ou eixo ).
Para calcular a componente em x do primeiro vetor, temos o seguinte:
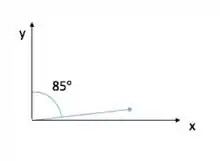
Como o ângulo se refere ao ângulo que ela faz com o eixo , temos que a componente em será o módulo do vetor multiplicado por (e não por um cosseno como estamos acostumados)!
Logo, teremos:
Passo 4
Agora vamos analisar componente por componente, começando pela componente para o norte (ou eixo ):
Passo 5
Para calcular o módulo, vamos usar a fórmula das componentes:
Passo 6
A ângulo do vetor, em relação ao norte, é:
Como o do ângulo é negativo e o do ângulo é positivo, o ângulo está no quarto quadrante.
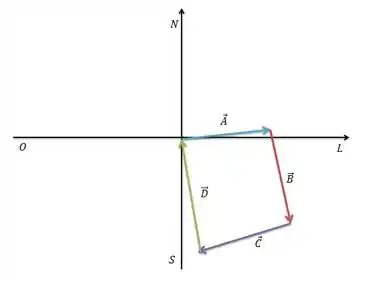
Repare que agora o quarto quadrante é o quadrante formado pelo eixo negativo e o positivo:
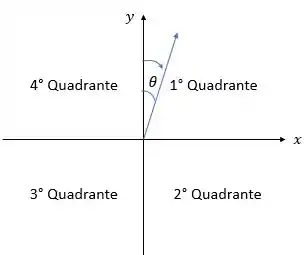
Isso porque estamos iniciando a contagem a partir o eixo , que é o norte, e vai no sentido horário. Normalmente, a gente inicia do eixo positivo e vai em sentido anti-horário... Beleza?? Só para não confundir!
Resposta
a)
b)