Um paciente em terapia tem um antebraço que pesa e que levanta um peso de . Essas duas forças têm direção verticalmente para baixo. As únicas outras forças significativas em seu antebraço vêm do músculo bíceps (que age perpendicularmente ao antebraço) e da força no cotovelo. Se o bíceps produz um impulso de quando o antebraço é levantado acima da horizontal, encontre a magnitude e direção da força que o cotovelo exerce no antebraço (A soma da força do cotovelo e da força do bíceps deve equilibrar o peso do braço e o peso que este está carregando, portanto, sua soma vetorial deve ser de , para cima.)
Passo 1
Olá pessoal, como vai a vida? Espero que esteja bem! Vamos pra mais uma questão??
Temos que um paciente cujo o seu antebraço pesa levanta um peso de .
Além dessas duas forças temos que levar em consideração a força do bíceps que quando o antebraço se encontra no ângulo de essa passa a ter valor de e a força que o cotovelo exerce.
Então com essas informações devemos encontrar justamente a magnitude e a direção dessa força exercida pelo cotovelo.
Em síntese temos o seguinte esquema:
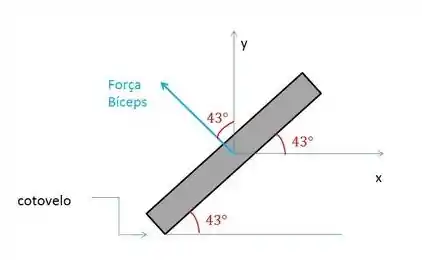
Qual é o jeito menos assustador de começar essa questão? hahaha
Na verdade vai ser bem tranquilo, bora lá!
Passo 2
Vamos começar decompondo as forças em relação ao eixo x:
Lembrando que decompor aqui significa projetar as forças em relação a cada eixo, por isso algumas relações trigonométricas serão importantes!
Quais são as forças que possuem componentes horizontais???
Boa, só são duas!!! São elas a força do bíceps e a força do cotovelo. Assim,
O sinal de se dá pelo fato da componente apontar para o lado negativo do eixo x.
Uma vez que o sistema só possui essas duas forças na horizontal e que tem que estar em equilíbrio:
Passo 3
Agoraaaa vamos decompor as forças em relação ao eixo y:
Como as componentes e devem no mínimo equilibrar a soma das forças do peso do antebraço juntamente com o peso do equipamento. Podemos concluir que
Obaaa, já temos as duas componentes de !!!
Para encontrar a magnitude basta utilizarmos o Teorema de Pitágoras já que o vetor e suas componentes formam um triângulo retângulo.
Passo 4
E por fim, agora precisamos só encontrar a direção da força que o cotovelo exerce.
E dá pra fazer isso?? Como??

Não é tãooo complicado, basta utilizarmos a tangente do ângulo que queremos encontrar.
Encontramos o valor da tangente mas queríamos mesmo era o valor do ângulo e agora??? Chorar não é uma opção hahaha.
Vamos utilizar a função arco-tangente que ela rapidinho resolve o nosso problema.
em relação ao eixo 0x
Prontinhoooo, conseguimos!
Bora continuar treinando que o 10 vem!
Resposta
Magnitude :
Direção: em relação ao eixo 0x