Um carro anda para o leste, depois para o sul, depois para o oeste e, finalmente, para o norte.
- Desenhe o vetor deslocamento correspondente à posição final do carro
- Qual o módulo deste vetor e qual o ângulo formado por ele com o eixo oeste-leste?
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema deu uma série de direções que um carro fez:
“ para o leste, depois para o sul, depois para o oeste e, finalmente, para o norte.”
Antes de mais nada, que tal transformar essas informações para vetores?

Vamos começar definindo que em um sistema cartesiano de coordenadas, as direções podem ser representadas por vetores unitários respectivamente:
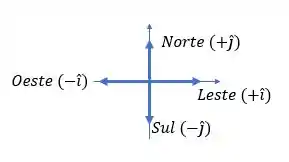
Sendo assim, podemos reescrever as direções do carro em termos desses vetores:
Tudo bem até aqui?
A ideia para resolver essa questão é justamente utilizar esses vetores para determinar o deslocamento final e o ângulo que o vetor faz com o eixo
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Letra (a): O legal de ser um vetor é que sua direção/sentido nunca vai mudar, mas podemos colocá-lo em qualquer lugar! Sendo assim, vamos desenhar os vetores deslocamento em um sistema cartesiano e verificar onde é o ponto final desse carro
Recapitulando os deslocamentos:
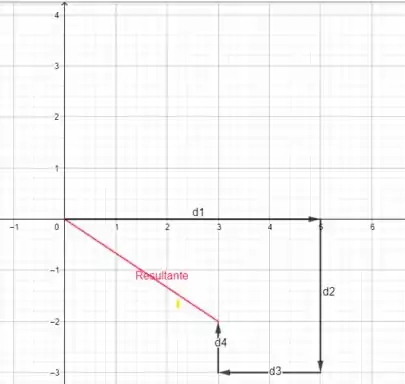
O deslocamento resultante está representado pelo segmento de reta vermelho e une o ponto inicial do primeiro vetor com a ponta do último vetor
Assim podemos ver que o deslocamento final tem as seguintes coordenadas
Beleza? Vamos para a letra (b)?
Passo 3
Letra (b) agora que sabemos as componentes do vetor resultante, podemos calcular o módulo e o ângulo que ele faz com o eixo :

Do passo anterior
Então , assim o módulo e o ângulo são
Show! E é isso pessoal! Espero ter ajudado!