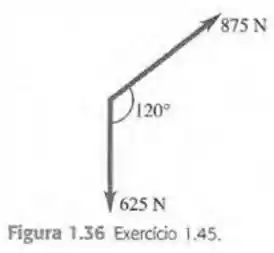
Use componentes de vetores para determinar o módulo e a direção do vetor necessários para equilibrar os dois vetores demonstrados na Figura . Considere o vetor ao longo do eixo e considere o eixo ortogonal a ele, no sentido da direita.
Passo 1
O primeiro passo da questão é achar o vetor resultante da soma dos vetores dados. Depois que acharmos o vetor resultando, para estar equilíbrio, as componentes precisam ser nulas, ou seja, basta adicionarmos um vetor contrário ao vetor resultante.
Passo 2
Para somar dois vetores vamos decompor cada um deles, para isso, podemos observa-los de uma outra forma:
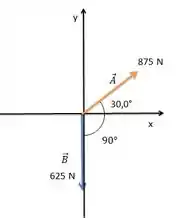
Decompondo o vetor :
Decompondo o vetor
Passo 3
Assim, o vetor resultante da soma dos vetores
Passo 4
Como o vetor necessário equilibrar precisa ser oposto ao vetor resultante temos:
Passo 5
Para calcular o módulo do vetor vamos usar suas componentes:
Passo 6
Para saber o sentido e a direção do vetor, vamos usar suas componentes para saber o ângulo em relação ao eixo
Calculando na sua calculadorazinha, você vai achar:
Mas CALMA AÍ, antes tem que dar uma olhada nas componentes!
Como a componente em é positiva e a componente é negativa, o vetor está no segundo quadrante. Logo: