Dado e , encontre a direção de relativo ao eixo .
A) no sentido anti horário
B) no sentido anti horário
C) no sentido anti horário
D) no sentido anti horário
E) no sentido anti-horário
Passo 1
Opa!! Vamos lá!
Se o e o , então o vai ser:
Show! Sabemos como é o vetor ... Mas como descobrimos o ângulo entre esse vetor e o eixo x???
Passo 2
Vamos desenhar esse vetor:
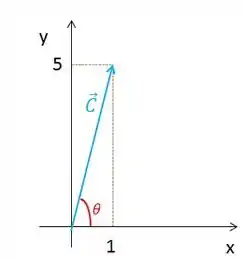
Podemos fazer a tangente do ângulo:
Então o vale:
Então:
Que é a letra A!
Resposta
Alternativa A.
Exercícios de Livros Relacionados
Um explorador polar foi surpreendido por urna nevasca, que reduziu a visibilidade a praticamente zero, quando retornava ao acampamento. Para chegar ao acampamento, deveria ter caminhado 5,6k m para o
Em um jogo de xadrez ao ar livre, no qual as peças ocupam o centro de quadrados com 1,00m de lado, um cavalo é movido da seguinte forma: (1) dois quadrados para a frente e um quadrado para a direita;
Um vetor deslocamento r → no plano x y tem 15m de comprimento e faz um ângulo θ = 30 ° com o semieixo x positivo, como mostra a Fig 3-26. Determine (a) a componente x e (b) a componente y do vetor.
Quais são (a) a componente x e (b) a componente y de um vetor a → do plano x y que faz um ângulo de 250 ° no sentido anti-horário com o semieixo x positivo e tem um módulo de 7,3m ?
Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano x y . As componentes ( x e y ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: 30,0