UnB - Listas - Física 1 - Lista 3 Vetores - Questão 5a
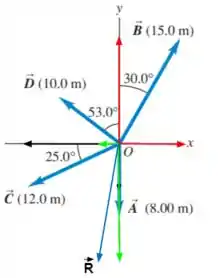
Encontre a magnitude e a direção do vetor que é a soma dos três vetores na figura abaixo. Em uma diagrama, mostre como é formado a partir desses três vetores.
Passo 1
Oiiiii pexuallllll! Tudo tranquilo?
Temos que encontrar o vetor resultante que representa a soma dos vetores e em seguida devemos representar como esse vetor é formado a partir dos outros 3 vetores. Vocês tem alguma ideia de como podemos começar essa questão?
Acho válido começamos decompondo cada um dos vetores…
Lembrando que a tarefa de decompor vetores é o fato de projetar aquele determinado vetor sobre o eixo cartesiano e por isso se faz o uso das relações trigonométricas fundamentais.
Assim, vamos começar decompondo os vetores em relação ao eixo x:
Detalhe, observem que o vetor está totalmente sobre o eixo y não tendo assim componente sobre o eixo x. E além disso, lembrem se a componente apontar para os eixos negativos o sinal de terá de ser acrescentado.
Passo 2
Agora faremos a decomposição para o eixo y:
Passo 3
Como já encontramos as componentes de agora para achar de fato a sua magnitude basta aplicarmos o teorema de Pitágoras, já que as componentes de um vetor formam com o mesmo um triângulo retângulo.
Passo 4
Passo 5
Passo 6
Agoraaaaa só falta encontrar a direção, ou melhor o ângulo, em que esse vetor se encontra em relação a vertical.
Podemos fazer isso utilizando a função tangente já que nos passos anteriores encontramos as componentes e vimos que essas formam um triângulo entre si.
Mas estamos interessados no ângulo em si e não na sua tangente, assim, vamos utilizar a função arco-tangente para resolver esse abacaxi.
em relação ao eixo -y
Já acabou Jéssica?
Nãoooo, ainda falta fazer o diagrama incluído a resultante .
Passo 7
Bora lá! Vamos representar todas as componentes dos vetores que geram o vetor .
Para evitar poluição visual foi as componentes do vetor na cor vermelha e as componentes de na cor preto.
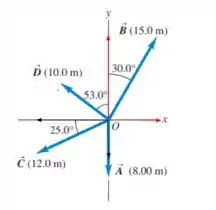
Após fazer-se a soma dos vetores que apontam no mesmo sentido e a subtração dos que apontam em sentidos contrários eis que surgem as componentes do vetor representadas na cor verde. É notável que o desenho corrobora com os nossos cálculos já que o ângulo que o vetor faz com a vertical é bem pequeno.
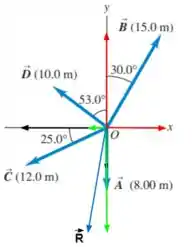
Resposta
em relação ao eixo -y
