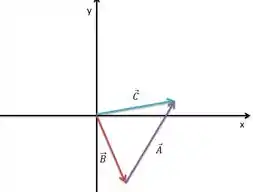
Você deseja programar o movimento do braço de um robô em uma linha de montagem para se mover no plano . Seu primeiro deslocamento é ; seu segundo deslocamento é , cujo módulo é igual a , formando um ângulo de , medido considerando-se uma rotação do eixo para o eixo . A resultante dos dois deslocamentos deve também possuir módulo igual a , porém formando um ângulo de , medido considerando-se uma rotação de eixo para o eixo .
- Desenhe um diagrama para escala aproximada para estes vetores.
- Ache os componentes de
- Ache o módulo e a direção de
Dados:
Passo 1
Bom, sabemos que a partir de módulo de um vetor e do seu ângulo conseguimos todas as informações das componentes dele, certo? Foi dado no problema:
Assim podemos decompor cada vetore e analisar suas componentes. Vamos fazer o movimento do robô?

Passo 2
Alternativa a)
Pra fazer esse diagrama vamos fazer primeiro o vetor e depois o vetor que são os vetores que nós conhecemos. Vamos usar o método geométrico.
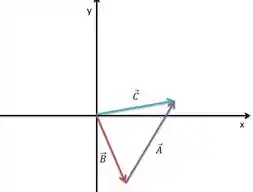
Passo 3
Alternativa b)
Decompondo o vetor .
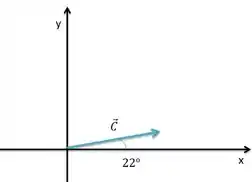
Substituindo os valores temos:
Passo 4
Decompondo o vetor .
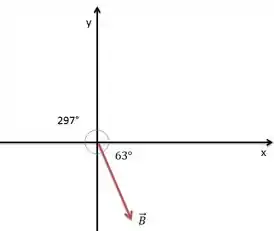
Substituindo os valores temos:
Passo 5
Assim, substituindo na equação os valores das componentes do vetor , temos:
Analisando cada componente separadamente temos:
Assim:
Passo 6
Alternativa c)
Para achar o módulo de vamos usar aquela fórmula das componentes, se lembra?
Substituindo os valores temos:
Passo 7
Para achar o ângulo, só pela componentes já da pra saber que ele está no primeiro quadrante.
Tirou isso da onde ???????
As duas componentes são positivas, ou seja, o seno e o cosseno do ângulo do vetor são positivos.
Agora vamos usar as componentes para achar o ângulo:
Fazendo o cálculo desse ângulo pela calculadora, vamos ter que:
Resposta