![]()
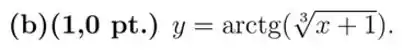
Passo 1
Vamos usar a Regra da Cadeia nesse cara aí:
Essa derivada que apareceu aí sai pela Regra da Cadeia também:
Pois .
Passo 2
Com isso, a derivada de será:
![]()
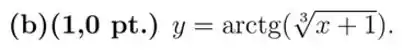
Vamos usar a Regra da Cadeia nesse cara aí:
Essa derivada que apareceu aí sai pela Regra da Cadeia também:
Pois .
Com isso, a derivada de será: