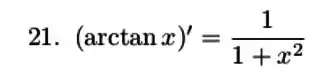
Passo 1
Nossa função é
Daí tiramos que
E sabemos que
Assim
Passo 2
Isolando o na relação que acabamos de encontrar, temos
E, da relação fundamental da trigonometria, temos que
Substituindo a relação do seno,
Colocando cosseno em evidencia:
Passo 3
Agora, vamos voltar a primeira relação que encontramos lá no passo 1:
Derivando ambos os lados em relação a :
Assim,
Passo 4
Opa! Mas no passo 2 a gente achou que
Substituindo isso então, ficamos com
E quem é ?
Isso mesmo, jovem Padawan, é a derivada da nossa função , que é justamente
Então
E demonstramos, uhul!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Resolva o exercício 54 da série de exercícios 8.1, mostrando que arctan x e - arctan 1 x diferem por uma constante e então calcule-a.
Dois pontos, A e B , são diametralmente opostos nas praias de um lago circular com 1 km de diâmetro. Uma pessoa deseja ir do ponto A ao ponto B . Ela pode remar a uma velocidade de 1 1 2 km/h e andar
Encontre a derivada da função dada:f (x) = sec^(- 1) (sqrt(x^2 + 4))
Encontre a derivada da função dada:f (x) = ln (tg^(- 1) 3 x)
Encontre a derivada da função dada:g (x) = x^2 sec^(- 1) (1)/(x)